www.kaggle.com/janiobachmann/credit-fraud-dealing-with-imbalanced-datasets
Credit Fraud || Dealing with Imbalanced Datasets
Explore and run machine learning code with Kaggle Notebooks | Using data from Credit Card Fraud Detection
www.kaggle.com
위 캐글러의 코드를 사용해 신용카드 부정사용 여부를 탐지하는 알고리즘을 공부해보려 한다.
일반적으로 신용카드사에서는 FDS(Fraud Detection System)라고 불리는 이상거래 탐지 시스템을 두고 있다고 한다.
카드 사용을 실시간으로 검토해 평상시 고객의 거래/사용내역과 현저히 다를 경우, 이를 이상거래로 인식하고 탐지해 카드 사용을 중단하도록 해서 고객의 혹시 모를 추가적인 피해를 방지하는 것이다.
예로 들만한 일화가 있는데, 아메리칸 익스프레스 블랙 카드를 사용하는 초vip 고객의 거래 내역에 포켓몬 고 휴대폰 소액결제 거래가 있어서 카드사에서는 이를 부정거래로 인식하고 카드 사용을 중지시킨 다음 고객에게 안내했는데, 알고보니 고객이 그 카드로 소액결제한 것이 맞아서 카드 사용 중지가 해제된 해프닝이 있었다.
이 일화는 특별한 케이스에 해당하지만, 실제로 카드를 도난당하거나 타인이 카드를 점유물이탈횡령하는 경우 발생하는
거래에서도 고객의 일상적인 거래 내역과 다른 패턴이 존재한다고 한다.
바로 그 이상 패턴을 감지하여 이상거래를 탐지하는 것이 이번 분석의 목표다.
하지만 부정거래의 수는 일반적인 거래의 수와 비교하자면 매우 적은 비중을 차지한다.
실제로 이번 분석에 사용할 "creditcard.csv" 데이터에서도 부정거래 케이스는 전체 데이터 중 0.17%로 매우 적다.
우리는 이러한 데이터를 Imbalanced data(불균형 데이터)라고 부르고 일반적인 성능 평가 척도인 정확도를 대신해 Precision(정밀도), Recall(재현율), F-1 score (F-1 점수)를 사용한다.
만약 불균형 데이터에서도 정확도를 성능 평가 지표로 사용한다면, 모델이 모든 test set을 부정거래가 아니라고 예측하더라도 대부분의 케이스는 부정거래가 아니기 때문에 정확도는 99%를 넘어갈 것이다.
Precision, Recall, F-1 score는 불균형 데이터에서 정확도를 대신하는 성능 평가의 척도이다.
또한, 불균형 데이터는 적은 케이스로 인해 모델링 성능의 신뢰도가 떨어진다는 문제가 있다.
이 문제를 해결하기 위해서 사용하는 대표적인 샘플링 방법 두 가지가 있다.
먼저, 많은 케이스(부정거래가 아닌 케이스)를 적은 케이스(부정거래 케이스)의 빈도에 맞추어 샘플링하는 Undersampling 방식이 있다.
그리고 적은 케이스(부정거래 케이스)를 많은 케이스(부정거래가 아닌 케이스)의 빈도에 맞추어 복제하는 Oversampling 방식이 있다.
Undersampling과 Oversampling에는 여러가지 기법이 존재하는데 이는 나중에 데이터에 직접 적용하며 배워보려 한다.
언더샘플링과 오버샘플링은 서로 다른 단점을 갖고 있다.
언더샘플링은 많은 케이스를 대부분 버려야하기 때문에 정보의 손실량이 매우 크다는 단점이 있다.
오버샘플링은 적은 케이스를 일종의 복제과정을 거쳐서 빈도수를 맞추기 때문에 과적합 되기가 쉽다.
따라서, 각 방식의 단점까지 고려해 데이터에 적합한 방식을 적용해야 할 것이다.
이번 분석은 다음의 순서대로 진행할 것이다.
I. 데이터 살펴보기
1) 데이터에 대한 이해
II. 전처리
1) 스케일링
2) 데이터 나누기
III. 랜덤 언더샘플링과 오버샘플링
1) 상관관계
2) 이상치 확인 및 제거
3) 차원축소와 군집화 (t-SNE)
4) 분류기
5) 로지스틱 회귀 깊이 알아보기
6) SMOTE를 사용한 오버샘플링
IV. 검증(Testing)
1) 로지스틱 회귀모형으로 검증(Test)
2) 신경망으로 검증 (언더샘플링과 오버샘플링 비교)
이제 데이터를 살펴보자.
1. 데이터 살펴보기
#Imported Libraries
import numpy as np
import pandas as pd
import tensorflow as tf
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.manifold import TSNE
from sklearn.decomposition import PCA, TruncatedSVD
import matplotlib.patches as mpatches
import time
#Classifier Libraries
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
import collections
#Other Libraries
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from imblearn.pipeline import make_pipeline as imbalanced_make_pipeline
from imblearn.over_sampling import SMOTE
from imblearn.under_sampling import NearMiss
from imblearn.metrics import classification_report_imbalanced
from sklearn.metrics import precision_score, recall_score, f1_score, roc_auc_score, accuracy_score,
classification_report
from collections import Counter
from sklearn.model_selection import KFold, StratifiedKFold
import warnings
warnings.filterwarnings("ignore")
df = pd.read_csv('./creditcard.csv')
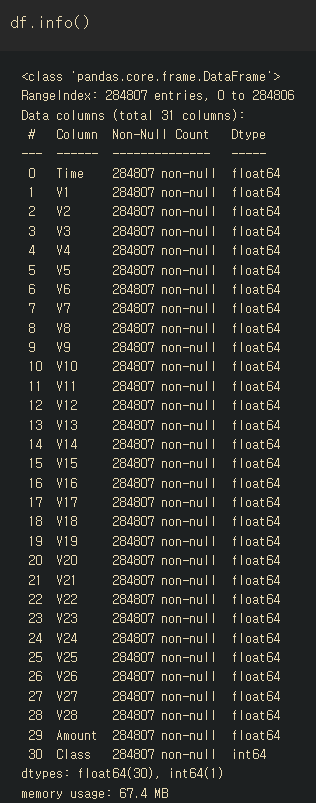
df.head()라이브러리를 몽땅 불러왔다.
주어진 데이터는 민감한 고객정보를 담고있어 PCA로 차원축소된 칼럼을 담고 있다.
칼럼명은 Class(부정거래여부)과 amount(거래금액), Time(시간) 그리고 의미를 알 수 없는 V1~V28로 구성되어있다.
따라서 V1부터 V28에 해당하는 칼럼이 어떤 의미가 있는 칼럼인지 전혀 파악할 수 없는 상황이다.
우리가 아는 부분은 이 알 수 없는 칼럼들이 모두 PCA로 Scaling 되어있다는 것.
#결측치 확인
df.isnull().sum().max()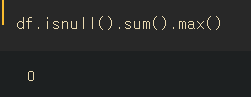
# Class 변수의 범주 비중 보기
print('No Frauds', round(df['Class'].value_counts()[0]/len(df) * 100, 2), '% of the dataset')
print('Frauds', round(df['Class'].value_counts()[1]/len(df) * 100, 2), '% of the dataset')
# Class 변수 시각화
colors = ['#0101DF', '#DF0101']
sns.countplot('Class', data = df, palette = colors)
plt.title('Class Distributions \n (0: No Fraud || 1: Fraud)', fontsize = 14)
#Amout, Time 변수의 분포 시각화
fig, ax = plt.subplots(1, 2, figsize = (18, 4))
amount_val = df['Amount'].values
time_val = df['Time'].values
sns.distplot(amount_val, ax = ax[0], color = 'r')
ax[0].set_title('Distribution of Transaction Amount', fontsize = 14)
sns.distplot(time_val, ax = ax[1], color = 'b')
ax[1].set_title('Distribution of Transaction Time', fontsize = 14)
ax[1].set_xlim([min(time_val), max(time_val)])
2. Preprocessing(전처리)
2-1. Scaling and Distributing
V1-V28 칼럼은 PCA가 진행되어 scaling 되어있지만, Time과 Amount 피쳐는 스케일링 되지 않은 상태이기 때문에 이 두 피쳐도 다른 칼럼처럼 스케일링을 진행해주려고 한다.
그리고 캐글러는 이 단계에서 Class의 부정거래 케이스를 균등하게 맞춰주기 위한 서브샘플링을 실시한다.
이 데이터에서 서브샘플(Sub-Sample)이란, 부정거래와 부정거래가 아닌 거래를 50대 50으로 균등한 비율로 만드는 것이다.
서브샘플을 만듦으로써 과적합 문제를 해결하고, Class와 각 피쳐 사이의 올바른 상관관계를 만들고자 한다.
#RobustScaler를 활용해서 변환
from sklearn.preprocessing import StandardScaler, RobustScaler
#RobustScaler는 이상치에 둔감하다.
std_scaler = StandardScaler()
rob_scaler = RobustScaler()
df['scaled_amount'] = rob_scaler.fit_transform(df['Amount'].values.reshape(-1, 1))
df['scaled_time'] = rob_scaler.fit_transform(df['Time'].values.reshape(-1, 1))
df.drop(['Time', 'Amount'], axis = 1, inplace = True)이상치에 둔감한 RobustScaler()를 사용해 scaled_amount, scaled_time이라는 변수를 만들었다.
RobustScaler().fit_transform(데이터['칼럼'].values(reshape(하한, 상한))
-> 칼럼의 모든 값들을 RobustScaler 방식을 사용하여 변환( .fit_transform() )한다.
reshape(-1, 1)은 series형처럼 하나의 열로 재배열하는 것이다.
StandardScaler는 안 쓸 거면서 왜 불러왔나 싶다.
#스케일링한 amount, time 변수 칼럼인덱스를 0, 1로 지정해 df에 삽입
scaled_amount = df['scaled_amount']
scaled_time = df['scaled_time']
df.drop(['scaled_amount', 'scaled_time'], axis = 1, inplace = True)
df.insert(0, 'scaled_amount', scaled_amount)
df.insert(1, 'scaled_time', scaled_time)
df.head()df.insert(0, 'scaled_amount', scaled_amount)
-> df라는 데이터에 'sclaed_amount'라는 칼럼명으로 scaled_amount를 삽입할 것인데 이 때 index = 0으로 지정한다.
즉, scaled_amount 칼럼을 가장 첫번째 칼럼으로 삽입

2-2. Splitting the Data (데이터 분할)
#2-2. Splitting the data
#데이터 분할
from sklearn.model_selection import StratifiedShuffleSplit
X = df.drop('Class', axis = 1)
y = df['Class']
sss = StratifiedKFold(n_splits = 5, random_state = None, shuffle = False)
for train_index, test_index in sss.split(X, y):
print("Train:", train_index, "Test:", test_index)
original_Xtrain, original_Xtest = X.iloc[train_index], X.iloc[test_index]
original_ytrain, original_ytest = y.iloc[train_index], y.iloc[test_index]
#라벨마다 분포 확인하기
original_Xtrain = original_Xtrain.values
original_Xtest = original_Xtest.values
original_ytrain = original_ytrain.values
original_ytest = original_ytest.values
#trian, test 라벨 분포
train_unique_label, train_counts_label = np.unique(original_ytrain, return_counts = True)
test_unique_label, test_counts_label = np.unique(original_ytest, return_counts = True)
print('-' * 100)
print('Label Distributions: \n')
print(train_counts_label/ len(original_ytrain))
print(test_counts_label/ len(original_ytest))sss = StratifiedKFold(n_splits = 5, random_state = None, shuffle = False)
-> sss라는 이름으로 층화 5-fold 샘플링을 하라는 뜻인듯.
for train_index, test_index in sss.split(X, y):
-> X(피쳐)랑 y(Class)를 층화 5-fold로 분할할건데 그 분할한 인덱스를 train_index, test_index로 구분(?)
orignal_Xtrain, original_Xtest = X.iloc[train_index], X.iloc[test_index]
-> iloc함수는 인덱스로 위치를 찾아주는 함수다. 저장된 train_index를 이용해 original_Xtrain이라는 이름으로 원래의 Xtrain 데이터를 만들어주고, 마찬가지로 test데이터에 대해서도 실시한다.
train_unique_label, train_counts_label = np.unique(original_ytrain, return_counts = True)
-> numpy의 unique()함수는 배열 내에서 중복된 원소를 제외하고 유일한 원소들을 정렬해서 반환한다.
return_counts 옵션은 각 요소들이 입력 배열에 나타난 횟수를 반환한다.
train_unique_label로 유일한 원소를 저장하고, train_counts_label에 각 원소의 카운트를 저장한다.
즉, original_ytrain에서 0아니면 1이기 때문에 train_unique_labe은 [0, 1]이 될 것이고
train_counts_label에서 각 카운트를 집계한다.
print(train_counts_label/ len(original_ytrain))
-> 0에대한 카운트와 1에대한 카운트를 각각 전체 데이터로 나눈다.
3. Random Under-Sampling
3-1. 언더샘플링
언더샘플링에서도 랜덤언더샘플링 방식은 불균형 데이터를 균형 데이터로 만들어주기 위해서 데이터를 제거하는 방식이다.
랜덤 언더샘플링의 절차는 다음과 같다.
1) 데이터가 얼마나 불균형한지 value_counts()로 확인
2) 많은 클래스를 적은 클래스에 맞추어 50대 50 비율로 맞춘다.
3) 각 클래스 별로 비율이 같아졌다면, 데이터를 섞어준다.
언더샘플링의 치명적인 단점은 적은 클래스에 맞추기 때문에 발생하는 정보의 손실이다.
creditcard 데이터에서도 언더샘플링을 사용하게 된다면, fraud = 1(이상거래)인 데이터 492개에 맞추어 fraud = 0(이상거래가 아닌 거래)인 데이터 492개를 랜덤하게 택하게 된다. 선택된 데이터 외의 나머지는 삭제해야하고 그 순간 무려 284,315개의 거래 데이터를 사용할 수 없게 된다.
언더샘플링을 사용할 때에는 이 점을 항상 주의하자.
#3-1. 랜덤 언더샘플링
df = df.sample(frac = 1)
#이상거래인 492개의 행
fraud_df = df.loc[df['Class'] == 1]
non_fraud_df = df.loc[df['Class'] == 0][:492]
normal_distributed_df = pd.concat([fraud_df, non_fraud_df])
#데이터 셔플
new_df = normal_distributed_df.sample(frac = 1, random_state = 42)
new_df.head()df = df.sample(frac = 1)
-> sample 함수를 써서 랜덤으로 추출한다. frac 옵션은 전체 데이터에서 추출할 비율을 뜻한다.
여기서는 frac = 1이므로 전체 데이터를 추출하는데 랜덤으로 추출했기 때문에 데이터가 섞이게 된다.
non_fraud_df = df.loc[df['Class'] == 0][:492]
-> 이상거래가 아닌 데이터 (Class = 0)들을 뽑아서, 그 중 1행부터 492행까지를 non_fraud_df로 저장한다.
normal_distributed_df = pd.concat([fraud_df, non_fraud_df])
-> concat함수를 사용하면 데이터프레임이 결합된다. 그 축의 디폴트값은 0으로 설정을 해주지 않으면 세로로 결합한다.
따라서, concat함수를 사용해 fraud_df와 non_fraud_df 데이터를 세로로 결합한 normal_distributed_df를 생성했다.
new_df = normal_distributed_df.sample(frac = 1, random_state = 42)
-> sample(frac = 1)이므로 normal_distributed_df 데이터 전체를 랜덤하게 섞어준다. random_state = 42는 일종의 난수표다. 이렇게 다시 섞어준 데이터를 new_df로 저장한다.
클래스 비율이 같아졌는지 확인해보자.
#클래스 비율이 동등해졌는지 확인
print('Distribution of the Classes in the subsample dataset')
print(new_df['Class'].value_counts()/len(new_df))
colors = ['#0101DF', '#DF0101']
sns.countplot('Class', data = new_df, palette = colors)
plt.title('Equally Distributed Classes', fontsize = 14)
plt.show()
언더샘플링 데이터에서 상관관계 행렬을 확인하는 것이 필수적이다.
상관관계를 봄으로써 어떤 피쳐가 이상거래에 영향을 미치는지 확인할 수 있기 때문이다.
하지만, 상관관계를 보기 위해서 적절한 서브샘플을 사용하는 것이 더 중요한 일이다.
#상관관계 행렬 시각화(heatmap)
f, (ax1, ax2) = plt.subplots(2, 1, figsize = (24, 20))
corr = df.corr()
sns.heatmap(corr, cmap = 'coolwarm_r', annot_kws = {'size' : 20}, ax = ax1)
ax1.set_title("Imbalanced Correlation Matrix \n (don't use for reference)", fontsize = 14)
sub_sample_corr = new_df.corr()
sns.heatmap(sub_sample_corr, cmap = 'coolwarm_r', annot_kws = {'size' : 20}, ax = ax2)
ax2.set_title('SubSample Correlation Matrix \n (use for reference)', fontsize = 14)
plt.show()ax1의 그래프는 전체 데이터의 상관관계 행렬이고 ax2는 서브샘플의 상관관계 행렬이다.
주의할 점)
서브샘플이 아니라 전체 데이터로 상관관계 행렬을 만들 경우에, 불균형한 데이터가 클래스에 영향을 미칠 수 있다.
따라서 서브샘플로 상관관계 행렬을 만들도록 하자.

서브샘플에서 봤을 때, V17, V14, V12, V10 등의 피쳐는 Class와 음의 상관관계를 갖는다.
즉, 이 피처 값이 낮을수록 이상거래 = 1일 확률이 높다.
V2, V4, V11, V19는 양의 상관관계를 갖는다.
이 피처 값이 높을수록 이상거래 = 1일 확률이 높다.
음의 상관관계를 갖는 피처와 클래스 변수의 박스플롯을 그려보자
#박스플롯 만들어서 비교
f, axes = plt.subplots(ncols = 4, figsize = (20, 4))
#클래스 변수와 음의 상관관계를 갖는 피쳐들의 박스플롯
colors = ['#0101DF', '#DF0101']
sns.boxplot(x = "Class", y = "V17", data = new_df, palette = colors, ax = axes[0])
axes[0].set_title("V17 vs Class Negative Correlation")
sns.boxplot(x = "Class", y = "V14", data = new_df, palette = colors, ax = axes[1])
axes[1].set_title("V14 vs Class Negative Correlation")
sns.boxplot(x = "Class", y = "V12", data = new_df, palette = colors, ax = axes[2])
axes[2].set_title("V12 vs Class Negative Correlation")
sns.boxplot(x = "Class", y = "V10", data = new_df, palette = colors, ax = axes[3])
axes[3].set_title("V10 vs Class Negative Correlation")
plt.show()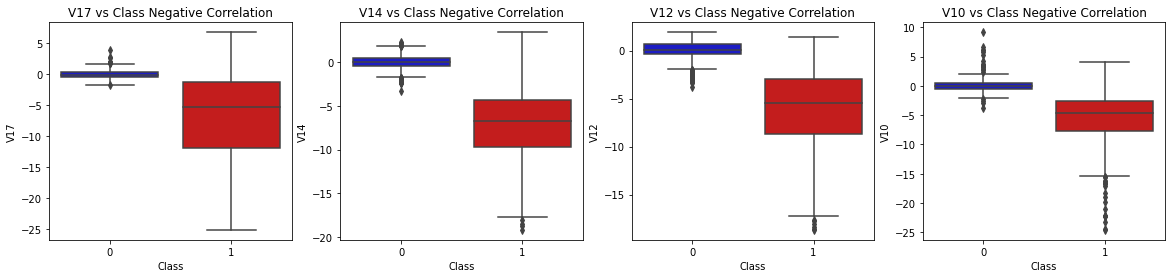
양의 상관관계를 갖는 피처와 클래스 변수의 박스플롯 그리기
#박스플롯 만들어서 비교
f, axes = plt.subplots(ncols = 4, figsize = (20, 4))
#클래스 변수와 양의 상관관계를 갖는 피쳐들의 박스플롯
colors = ['#0101DF', '#DF0101']
sns.boxplot(x = "Class", y = "V11", data = new_df, palette = colors, ax = axes[0])
axes[0].set_title("V11 vs Class Positive Correlation")
sns.boxplot(x = "Class", y = "V4", data = new_df, palette = colors, ax = axes[1])
axes[1].set_title("V4 vs Class Positive Correlation")
sns.boxplot(x = "Class", y = "V2", data = new_df, palette = colors, ax = axes[2])
axes[2].set_title("V2 vs Class Positive Correlation")
sns.boxplot(x = "Class", y = "V19", data = new_df, palette = colors, ax = axes[3])
axes[3].set_title("V19 vs Class Positive Correlation")
plt.show()
3-2. Anomaly Detection (이상치 확인)
이 단계의 목적은 클래스와 상관관계가 매우 높은 피처에서 극단적인 이상치(Extreme Outliers)를 제거하는 것이다.
이로써 우리가 만드는 모델의 정확성을 높이는 효과를 얻을 수 있다고 한다.
이상치를 판단하는 방법으로 IQR과 박스플롯을 사용한다.
이상치를 결정하는 한계점(threshold)은 보통 상한점 Q3 + 1.5 * IQR, 하한점은 Q1 - 1.5 * IQR로 통용된다.
IQR에 곱하는 계수를 달리함으로써 이상치를 더 적게 만들수도 있고, 더 많이 만들수도 있다.
만일 이 한계점을 낮추면 이상치가 많아질 것이고, 한계점을 높이면 이상치가 줄어들 것이다.
이러한 상충관계(반비례 관계)를 tradeoff라고 표현한다.
캐글러는 1.5 * IQR을 사용해 극단적인 이상치만 제거함으로써 정보의 손실을 최소화하고자 했다.
먼저, 이상치를 확인하기 위해 각 피처의 분포를 시각화한다.
시각화를 위해 seaborn 패키지의 distplot을 활용했다.
#3-2. Anomaly Detection (이상치 확인)
from scipy.stats import norm
f, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize = (20, 6))
v14_fraud_dist = new_df['V14'].loc[new_df['Class'] == 1].values
sns.distplot(v14_fraud_dist, ax = ax1, fit = norm, color = '#FB8861')
ax1.set_title('V14 Distribution \n (Fraud Transactions)', fontsize = 14)
v12_fraud_dist = new_df['V12'].loc[new_df['Class'] == 1].values
sns.distplot(v12_fraud_dist, ax = ax2, fit = norm, color = '#56F9BB')
ax2.set_title('V12 Distribution \n (Fraud Transactions)', fontsize = 14)
v10_fraud_dist = new_df['V10'].loc[new_df['Class'] == 1].values
sns.distplot(v10_fraud_dist, ax = ax3, fit = norm, color = '#C5B3F9')
ax3.set_title('V10 Distribution \n (Fraud Transactions)', fontsize = 14)
plt.show()v14_fraud_dist = new_df['V14'].loc[new_df['Class'] == 1].values
-> 서브샘플 데이터프레임의 V14 피처 중에서 ( new_df['V14'] ) 클래스가 1인 것을 추려서 ( .loc[new_df['Class'] == 1] )
그 값들( .values ) 을 v14_fraud_dist 에 저장하라.
sns.distplot(v14_fraud_dist, ax = ax1, fit = norm, color = '#FB8861')
-> seaborn패키지의 distplot 함수를 써서 v14_fruad_dist 에 대한 분포를 시각화하라. ( sns.distplot(v14_fraud_dist) )
서브플롯 중에 첫번째에다가 그걸 그리고 (ax = ax1) , 데이터 분포랑 비교할 수 있는 정규분포도 같이 그려라. ( fit = norm )

IQR범위의 계수를 1.5로 하여 극단적인 이상치를 제거해보자.
#극단적인 이상치 제거
#V14 이상치 제거
v14_fraud = new_df['V14'].loc[new_df['Class'] == 1].values
q25, q75 = np.percentile(v14_fraud, 25), np.percentile(v14_fraud, 75)
print('Quartile 25: {} | Quartile 75: {}'.format(q25, q75))
v14_iqr = q75 - q25
print('iqr: {}'.format(v14_iqr))
v14_cut_off = v14_iqr * 1.5
v14_lower, v14_upper = q25 - v14_cut_off, q75 + v14_cut_off
print('Cut Off: {}'.format(v14_cut_off))
print('V14 Lower: {}'.format(v14_lower))
print('V14 Upper: {}'.format(v14_upper))
outliers = [x for x in v14_fraud if x < v14_lower or x > v14_upper]
print('Feature V14 Outliers for Fraud Cases: {}'.format(len(outliers)))
print('V14 outliers: {}'.format(outliers))
new_df = new_df.drop(new_df[(new_df['V14'] > v14_upper) | (new_df['V14'] < v14_lower)].index)
print('----' * 44)
#V12 이상치 제거
v12_fraud = new_df['V12'].loc[new_df['Class'] == 1].values
q25, q75 = np.percentile(v12_fraud, 25), np.percentile(v12_fraud, 75)
print('Quartile 25: {} | Quartile 75: {}'.format(q25, q75))
v12_iqr = q75 - q25
print('iqr: {}'.format(v12_iqr))
v12_cut_off = v12_iqr * 1.5
v12_lower, v12_upper = q25 - v12_cut_off, q75 + v12_cut_off
print('Cut Off: {}'.format(v12_cut_off))
print('V12 Lower: {}'.format(v12_lower))
print('V12 Upper: {}'.format(v12_upper))
outliers = [x for x in v12_fraud if x < v12_lower or x > v12_upper]
print('Feature V12 Outliers for Fraud Cases: {}'.format(len(outliers)))
print('V12 outliers: {}'.format(outliers))
new_df = new_df.drop(new_df[(new_df['V12'] > v12_upper) | (new_df['V12'] < v12_lower)].index)
print('Number of Instances after outliers removal: {}'.format(len(new_df)))
print('----' * 44)
#V10 이상치 제거
v10_fraud = new_df['V10'].loc[new_df['Class'] == 1].values
q25, q75 = np.percentile(v10_fraud, 25), np.percentile(v10_fraud, 75)
print('Quartile 25: {} | Quartile 75: {}'.format(q25, q75))
v10_iqr = q75 - q25
print('iqr: {}'.format(v10_iqr))
v10_cut_off = v10_iqr * 1.5
v10_lower, v10_upper = q25 - v10_cut_off, q75 + v10_cut_off
print('Cut Off: {}'.format(v10_cut_off))
print('V10 Lower: {}'.format(v10_lower))
print('V10 Upper: {}'.format(v10_upper))
outliers = [x for x in v10_fraud if x < v10_lower or x > v10_upper]
print('Feature V10 Outliers for Fraud Cases: {}'.format(len(outliers)))
print('V10 outliers: {}'.format(outliers))
new_df = new_df.drop(new_df[(new_df['V10'] > v10_upper) | (new_df['V10'] < v10_lower)].index)
print('Number of Instances after outliers removal: {}'.format(len(new_df)))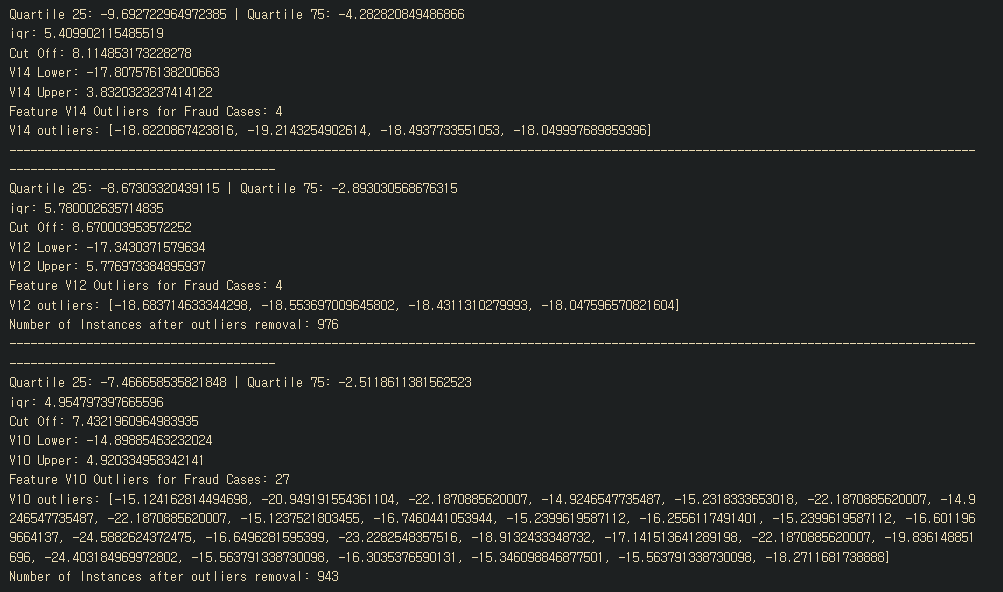
의문인 점은 캐글러랑 똑같은 개수의 이상치를 제거했는데, 캐글러는 이상치 제거 후 남은 개수가 947개인 반면 나는 943개가 남았다.
긴 시간동안 고민해봤지만 이 차이가 발생할만한 이유를 모르겠어서 일단 넘어가기로 했다.
이상치를 제거한 후의 박스플롯 확인
#이상치 제거 후의 박스플롯 확인
f, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize = (20, 6))
colors = ['#B3F9C5', '#f9c5b3']
#V14 박스플롯
sns.boxplot(x = 'Class', y = 'V14', data = new_df, ax = ax1, palette = colors)
ax1.set_title('V14 Feature \n Reduction of outliers', fontsize = 14)
ax1.annotate('Fewer extreme \n outliers', xy = (0.98, -17.5), xytext = (0, -12),
arrowprops = dict(facecolor = 'black'), fontsize = 14)
#V12 박스플롯
sns.boxplot(x = 'Class', y = 'V12', data = new_df, ax = ax2, palette = colors)
ax2.set_title('V12 Feature \n Reduction of outliers', fontsize = 14)
ax2.annotate('Fewer extreme \n outliers', xy = (0.98, -17.3), xytext = (0, -12),
arrowprops = dict(facecolor = 'black'), fontsize = 14)
#V10 박스플롯
sns.boxplot(x = 'Class', y = 'V10', data = new_df, ax = ax3, palette = colors)
ax3.set_title('V10 Feature \n Reduction of outliers', fontsize = 14)
ax3.annotate('Fewer extreme \n outliers', xy = (0.95, -16.5), xytext = (0, -12),
arrowprops = dict(facecolor = 'black'), fontsize = 14)
plt.show()
3-3. 차원축소와 클러스터링
t-SNE 알고리즘을 이해하기 위해서는 유클리드 거리, 조건부확률, 정규분포와 t-분포를 이해하고 있어야 한다.
나도 t-SNE 알고리즘은 처음 들어보는데 위 세가지는 알고 있으므로 바로 진행해보자.
t-SNE 알고리즘은 이상거래와 이상거래가 아닌 데이터를 제법 정확하게 군집화할 수 있는 알고리즘이다.
서브샘플이 1000개가 안 되는 데이터지만 t-SNE 알고리즘은 이렇게 적은 데이터로도 군집을 정할 수 있다.
이렇게 군집을 정함으로써 예측 모델이 분류할 때 더 잘 작동할 수 있도록 도와준다고 한다.
#3-3. 차원축소와 클러스터링
#알고리즘 적용에 걸리는 시간 측정
#t-SNE 알고리즘으로 군집화
X = new_df.drop('Class', axis = 1)
y = new_df['Class']
t0 = time.time()
X_reduced_tsne = TSNE(n_components = 2, random_state = 42).fit_transform(X.values)
t1 = time.time()
print("T-SNE too {:.2} s".format(t1 - t0))
#PCA 적용
t0 = time.time()
X_reduced_pca = PCA(n_components = 2, random_state = 42).fit_transform(X.values)
t1 = time.time()
print("PCA took {:.2} s".format(t1 - t0))
#Truncated SVD
t0 = time.time()
X_reduced_svd = TruncatedSVD(n_components = 2, algorithm = 'randomized',
random_state = 42).fit_transform(X.values)
print("Truncated SVD took {:.2} s".format(t1 - t0))
#클러스터링 시각화 (산점도)
f, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize = (24, 6))
f.suptitle('Clusters using Dimensionality Reduction', fontsize = 14)
blue_patch = mpatches.Patch(color = '#0A0AFF', label = 'No Fraud')
red_patch = mpatches.Patch(color = '#AF0000', label = 'Fraud')
#t-SNE 산점도
ax1.scatter(X_reduced_tsne[:, 0], X_reduced_tsne[:, 1], c = (y == 0), cmap = 'coolwarm',
label = 'No Fraud', linewidths = 2)
ax1.scatter(X_reduced_tsne[:, 0], X_reduced_tsne[:, 1], c = (y == 1), cmap = 'coolwarm',
label = 'Fraud', linewidths = 2)
ax1.set_title('t-SNE', fontsize = 14)
ax1.grid(True)
ax1.legend(handles = [blue_patch, red_patch])
#PCA산점도
ax2.scatter(X_reduced_pca[:, 0], X_reduced_pca[:, 1], c = (y == 0), cmap = 'coolwarm',
label = 'No Fraud', linewidths = 2)
ax2.scatter(X_reduced_pca[:, 0], X_reduced_pca[:, 1], c = (y == 1), cmap = 'coolwarm',
label = 'Fraud', linewidths = 2)
ax2.set_title('PCA', fontsize = 14)
ax2.grid(True)
ax2.legend(handles = [blue_patch, red_patch])
#truncated SVD 산점도
ax3.scatter(X_reduced_svd[:, 0], X_reduced_svd[:, 1], c = (y == 0), cmap = 'coolwarm',
label = 'No Fraud', linewidths = 2)
ax3.scatter(X_reduced_svd[:, 0], X_reduced_svd[:, 1], c = (y == 1), cmap = 'coolwarm',
label = 'Fraud', linewidths = 2)
ax3.set_title('Truncated SVD', fontsize = 14)
ax3.grid(True)
ax3.legend(handles = [blue_patch, red_patch])
plt.show()
뒤집혀서 나오긴 했는데.. 클러스터링 자체는 똑같이 된 것 같아서 넘어가기로 했다.
(추가)
알아보니 t-SNE 방식은 군집의 특성을 유지하면서 클러스터링 하는데, 매 계산마다 축의 위치가 바뀐다고 한다.
매번 값이 바뀌는 특성때문에 머신러닝 모델의 학습 피처로 사용하기는 어렵다.
3-4. 분류기 (언더샘플링)
캐글러는 이 단계에서부터 4개의 분류기를 적용해 어떤 분류기가 가장 효율적으로 예측하는지 알아보고자 했다.
분류 모델을 만들기 위해서는 먼저 우리의 데이터를 train, test set으로 나누고 피처로부터 라벨을 분리해야 한다.
참고)
우리가 사용할 분류기 중에서 로지스틱회귀 분류기는 사용할 다른 분류기보다 더 높은 정확도를 보인다.
그리드서치 교차검증을 써서 가장 예측 성능이 좋은 분류기의 parameter를 찾아줄 것이다.
로지스틱 회귀는 ROC커브 점수에서 가장 높은 점수를 보일 것이다.
#3-4. 분류기 (언더샘플링)
#피쳐와 클래스 나누기
X = new_df.drop('Class', axis = 1)
y = new_df['Class']
#위에서 이미 스케일링을 했기 때문에 바로 train, test split을 실시한다.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 42)
#분류기 알고리즘에 맞추기 위해 행렬로 만든다.
X_train = X_train.values
X_test = X_test.values
y_train = y_train.values
y_test = y_test.values
#분류기 만들기
classifiers = {
"LogisticRegression" : LogisticRegression(),
"KNearest" : KNeighborsClassifier(),
"Support Vector Classifier" : SVC(),
"DecisionTreeClassifier" : DecisionTreeClassifier()
}
#교차검증
from sklearn.model_selection import cross_val_score
for key, classifier in classifiers.items():
classifier.fit(X_train, y_train)
training_score = cross_val_score(classifier, X_train, y_train, cv = 5)
print("Classifiers: ", classifier.__class__.__name__, "Has a training score of",
round(training_score.mean(), 2) * 100, "% accuracy score")for key, classifier in classifiers.items():
-> 우리가 classifiers 라고 지정한 딕셔너리에서 각각의 key 값과 classifier에 대해서
classifier.fit(X_train, y_train)
-> 그 각각의 분류기에 대해서 X_train과 y_train 데이터로 모형을 적합시키고
training_score = cross_val_score(classifier, X_train, y_train, cv = 5)
-> 각 분류기를 X_train, y_train을 사용해 5-교차검증을 실시해라.
print("Classifiers: ", classifier.__class__.__name__, "Has a training score of", round(training_score.mean(), 2) * 100, "% accuracy score")
-> .__class__.__name__ 만 알면 될 것 같은데, 분류기의 이름을 출력해주는 함수라고 생각하면 될 것 같다.
그리드 서치 적용
#그리드서치 CV 쓰기
from sklearn.model_selection import GridSearchCV
#로지스틱 회귀
log_reg_params = {"penalty" : ['l1', 'l2'], 'C' : [0.001, 0.01, 0.1, 1, 10, 100, 1000]}
grid_log_reg = GridSearchCV(LogisticRegression(), log_reg_params)
grid_log_reg.fit(X_train, y_train)
log_reg = grid_log_reg.best_estimator_
#KNN
knears_params = {"n_neighbors" : list(range(2, 5, 1)),
'algorithm' : ['auto', 'ball_tree', 'kd_tree', 'brute']}
grid_knears = GridSearchCV(KNeighborsClassifier(), knears_params)
grid_knears.fit(X_train, y_train)
knears_neighbors = grid_knears.best_estimator_
#서포트벡터 분류기
svc_params = {'C' : [0.5, 0.7, 0.9, 1], 'kernel' : ['rbf', 'poly', 'sigmoid', 'linear']}
grid_svc = GridSearchCV(SVC(), svc_params)
grid_svc.fit(X_train, y_train)
svc = grid_svc.best_estimator_
#의사결정나무
tree_params = {"criterion" : ["gini", "entropy"], "max_depth" : list(range(2, 4, 1)),
"min_samples_leaf" : list(range(5, 7, 1))}
grid_tree = GridSearchCV(DecisionTreeClassifier(), tree_params)
grid_tree.fit(X_train, y_train)
tree_clf = grid_tree.best_estimator_네 가지 분류기의 하이퍼파라미터를 그리드로 정해서 만들어줌
#교차검증으로 과적합 줄이기
log_reg_score = cross_val_score(log_reg, X_train, y_train, cv = 5)
print('Logistic Regression CV Score: ', round(log_reg_score.mean() * 100, 2).astype(str) + '%')
knears_score = cross_val_score(knears_neighbors, X_train, y_train, cv = 5)
print('KNN CV Score: ', round(knears_score.mean() * 100, 2).astype(str) + '%')
svc_score = cross_val_score(svc, X_train, y_train, cv = 5)
print('Suppor Vector Classifier CV Score: ', round(svc_score.mean() * 100, 2).astype(str) + '%')
tree_score = cross_val_score(tree_clf, X_train, y_train, cv = 5)
print('Decision Tree Classifier CV Score: ', round(tree_score.mean() * 100, 2).astype(str) + '%')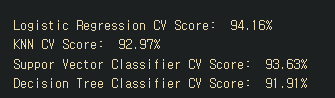
교차검증 중에 언더샘플링 하기
#교차검증과 동시에 언더샘플링하기
undersample_X = df.drop('Class', axis = 1)
undersample_y = df['Class']
sss = StratifiedKFold(n_splits = 5, random_state = None, shuffle = False)
for train_index, test_index in sss.split(undersample_X, undersample_y):
print("Train: ", train_index, "Test: ", test_index)
undersample_Xtrain, undersample_Xtest = undersample_X.iloc[train_index], undersample_X.iloc[test_index]
undersample_ytrain, undersample_ytest = undersample_y.iloc[train_index], undersample_y.iloc[test_index]
undersample_Xtrain = undersample_Xtrain.values
undersample_Xtest = undersample_Xtest.values
undersample_ytrain = undersample_ytrain.values
undersample_ytest = undersample_ytest.values
undersample_accuracy = []
undersample_precision = []
undersample_recall = []
undersample_f1 = []
undersample_auc = []
#NearMiss 기법 사용하기
#(어떻게 분배하는지 확인하는 용도이지, 변수로써 사용할 것은 아님)
X_nearmiss, y_nearmiss = NearMiss().fit_sample(undersample_X.values, undersample_y.values)
print('NearMiss Label Distribution: {}'.format(Counter(y_nearmiss)))
#올바른 CV
for train, test in sss.split(undersample_Xtrain, undersample_ytrain):
undersample_pipeline = imbalanced_make_pipeline(NearMiss(sampling_strategy = 'majority'),
log_reg) #SMOTE가 교차검증 전이 아닌 교차검증 중에 발생
undersample_model = undersample_pipeline.fit(undersample_Xtrain[train], undersample_ytrain[train])
undersample_prediction = undersample_model.predict(undersample_Xtrain[test])
undersample_accuracy.append(undersample_pipeline.score(original_Xtrain[test], original_ytrain[test]))
undersample_precision.append(precision_score(original_ytrain[test], undersample_prediction))
undersample_recall.append(recall_score(original_ytrain[test], undersample_prediction))
undersample_f1.append(f1_score(original_ytrain[test], undersample_prediction))
undersample_auc.append(roc_auc_score(original_ytrain[test], undersample_prediction))어후 너무 복잡하다..
교차검증과 동시에 언더샘플링을 하기위해 그동안 사용했던 new_df가 아닌 df를 다시 사용해서 피처와 클래스로 나눈다. -> 각각 undersample_X와 undersample_y로 저장
그리고 층화추출 방식으로 fold를 5개로 나눈다. 이를 위해서 인덱스를 저장해야 한다.
-> for train_index, test_index in sss.split(undersample_X, undersample_y):
print("Train", train_index, "Test:", test_index)
-> 그렇게 5개의 폴드로 나뉜 인덱스를 확인해보려고 굳이 출력한 것.

undersample_Xtrain, undersample_Xtest = undersample_X.iloc[train_index], undersample_X.iloc[test_index]
undersample_ytrain, undersample_ytest = undersample_y.iloc[train_index], undersample_y.iloc[test_index]
-> 폴드에서 지정한 인덱스를 사용해 각각 undersample_Xtrain과 undersample_Xtest로 저장한다.
y에 대해서도 같은 인덱스를 적용해 undersample_ytrain과 undersample_ytest로 각각 저장한다.
.values로 x, y 훈련, 검증 셋을 행렬로 바꿔준다.
그리고 우리는 성능평가 지표로 accuracy, precision, recall, f1, roc_auc 점수를 모두 사용할 것이다.
X_nearmiss, y_nearmiss = NearMiss().fit_sample(undersample_X.values, udersample_y.values)
-> X, y를 행렬화 해준 것을 섞어준 다음, Nearmiss 기법을 써서 제대로 추출이 되는지 확인해본다.
NearMiss() 함수는 imblearn 패키지의 함수 중 하나로 자동으로 언더샘플링을 해주는 함수다.
아마도 많은 케이스를 적은 케이스에 맞추어 주는 함수인 것 같다.
다범주에서도 지원한다고 하니 기억해두면 좋을 것 같다.
print('NearMiss Label Distribution: {}'.format(Counter(y_nearmiss)))
-> Counter() 함수는 collections 모듈의 함수이고, 리스트에 속하는 원소의 개수를 출력한다.

for train, test in sss.split(undersample_Xtrain, undersample_ytrain):
-> 층화 5폴드 방식으로 undersample_Xtrain과 undersample_ytrain 데이터를 나누어 train과 test로 저장한다.
undersample_pipeline = imbalanced_make_pipeline(NearMiss(sampling_strategy = 'majority'), log_reg)
-> imblearn 패키지의 pipeline 모듈에 있는 imbalanced_make_pipeline 함수를 사용해 파이프라인을 만든다.
NearMiss기법 중 sampling_strategy 옵션에 majority를 적용하고, 아까 위에서 만들었던 log_reg, 즉 로지스틱 회귀 모형 중에서 best_estimator로 나온 모델을 사용한다.
즉, 우리는 로지스틱 회귀모형에서 최적의 파라미터를 사용한 모델에 한해서 NearMiss 기법을 적용한 언더샘플링을 실시하는 것이다.
undersample_model = undersample_pipeline.fit(undersample_Xtrain[train], undersample_ytrain[train])
-> 만든 파이프라인에 undersample_Xtrain을 폴드로 나누었던 train 데이터와 undersample_ytrain을 폴드로 나누어 생긴 train 데이터를 사용해서 undersample_model을 만든다.
undersample_prediction = undersample_model.predict(undersample_Xtrain[test])
-> 예측은 undersample_model에 undersample_Xtrain 데이터를 폴드로 나누어 생긴 test 데이터에 적용한다.
undersample_accuracy.append(undersample_pipeline.score(original_Xtrain[test], original_ytrain[test]))
-> 이제 정확도를 산출해서 undersample_accuracy에 순서대로 저장할 건데(fold는 5개니까 5번 시행될 것임)
성능평가는 오리지널 데이터에 test를 적용해 위에서 만들어준 undersample_pipeline으로 성능평가를 실시한다.
정말 어렵고 복잡하게 느껴진다.
파이프라인, 모델명 등에서 undersample이라는 단어가 반복되면서 정리하면서도 무슨 말인지 헷갈린다.
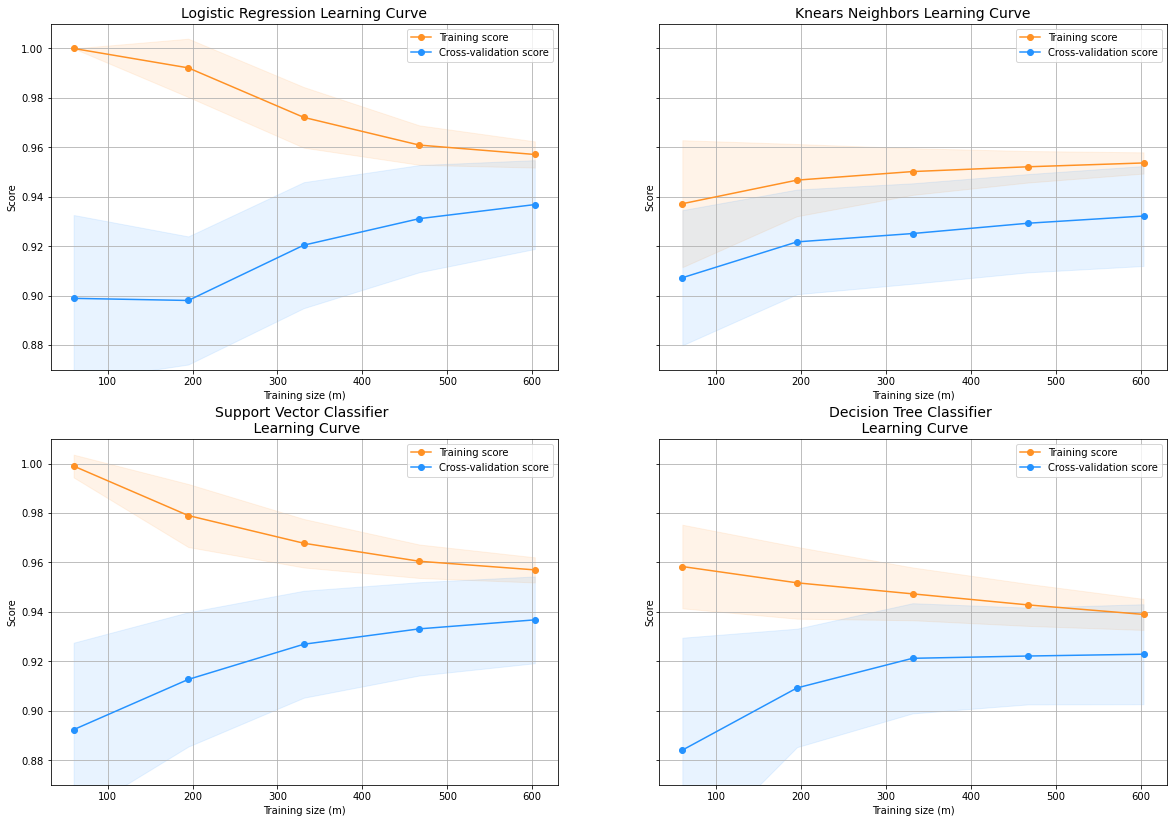
로지스틱 회귀 분류기의 학습곡선 그리기
#학습 곡선 그리는 함수 정의하기
from sklearn.model_selection import ShuffleSplit
from sklearn.model_selection import learning_curve
def plot_learning_curve(estimator1, estimator2, estimator3, estimator4, X, y, ylim = None, cv = None,
n_jobs = 1, train_sizes = np.linspace(.1, 1.0, 5)):
f, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, figsize = (20, 14), sharey = True)
if ylim is not None:
plt.ylim(*ylim)
#첫번째 estimator
train_sizes, train_scores, test_scores = learning_curve(estimator1, X, y, cv = cv,
n_jobs = n_jobs, train_sizes = train_sizes)
train_scores_mean = np.mean(train_scores, axis = 1)
train_scores_std = np.std(train_scores, axis = 1)
test_scores_mean = np.mean(test_scores, axis = 1)
test_scores_std = np.std(test_scores, axis = 1)
ax1.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha = 0.1, color = "#ff9124")
ax1.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha = 0.1, color = '#2492ff')
ax1.plot(train_sizes, train_scores_mean, 'o-', color = '#ff9124', label = 'Training score')
ax1.plot(train_sizes, test_scores_mean, 'o-', color = '#2492ff', label = 'Cross-validation score')
ax1.set_title("Logistic Regression Learning Curve", fontsize = 14)
ax1.set_xlabel('Training size (m)')
ax1.set_ylabel('Score')
ax1.grid(True)
ax1.legend(loc = 'best')
#두번째 estimator
train_sizes, train_scores, test_scores = learning_curve(estimator2, X, y, cv = cv,
n_jobs = n_jobs, train_sizes = train_sizes)
train_scores_mean = np.mean(train_scores, axis = 1)
train_scores_std = np.std(train_scores, axis = 1)
test_scores_mean = np.mean(test_scores, axis = 1)
test_scores_std = np.std(test_scores, axis = 1)
ax2.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha = 0.1, color = "#ff9124")
ax2.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha = 0.1, color = '#2492ff')
ax2.plot(train_sizes, train_scores_mean, 'o-', color = '#ff9124', label = 'Training score')
ax2.plot(train_sizes, test_scores_mean, 'o-', color = '#2492ff', label = 'Cross-validation score')
ax2.set_title("Knears Neighbors Learning Curve", fontsize = 14)
ax2.set_xlabel('Training size (m)')
ax2.set_ylabel('Score')
ax2.grid(True)
ax2.legend(loc = 'best')
#세번째 estimator
train_sizes, train_scores, test_scores = learning_curve(estimator3, X, y, cv = cv,
n_jobs = n_jobs, train_sizes = train_sizes)
train_scores_mean = np.mean(train_scores, axis = 1)
train_scores_std = np.std(train_scores, axis = 1)
test_scores_mean = np.mean(test_scores, axis = 1)
test_scores_std = np.std(test_scores, axis = 1)
ax3.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha = 0.1, color = "#ff9124")
ax3.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha = 0.1, color = '#2492ff')
ax3.plot(train_sizes, train_scores_mean, 'o-', color = '#ff9124', label = 'Training score')
ax3.plot(train_sizes, test_scores_mean, 'o-', color = '#2492ff', label = 'Cross-validation score')
ax3.set_title("Support Vector Classifier \n Learning Curve", fontsize = 14)
ax3.set_xlabel('Training size (m)')
ax3.set_ylabel('Score')
ax3.grid(True)
ax3.legend(loc = 'best')
#네번째 estimator
train_sizes, train_scores, test_scores = learning_curve(estimator4, X, y, cv = cv,
n_jobs = n_jobs, train_sizes = train_sizes)
train_scores_mean = np.mean(train_scores, axis = 1)
train_scores_std = np.std(train_scores, axis = 1)
test_scores_mean = np.mean(test_scores, axis = 1)
test_scores_std = np.std(test_scores, axis = 1)
ax4.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha = 0.1, color = "#ff9124")
ax4.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha = 0.1, color = '#2492ff')
ax4.plot(train_sizes, train_scores_mean, 'o-', color = '#ff9124', label = 'Training score')
ax4.plot(train_sizes, test_scores_mean, 'o-', color = '#2492ff', label = 'Cross-validation score')
ax4.set_title("Decision Tree Classifier \n Learning Curve", fontsize = 14)
ax4.set_xlabel('Training size (m)')
ax4.set_ylabel('Score')
ax4.grid(True)
ax4.legend(loc = 'best')
return plt이건 설명을 생략하기로 한다...
plot_learning_curve라는 함수를 정의해서 로지스틱, KNN, SVC, 트리 모형에서 최적의 모델을 적용해, X_train과 y_train을 사용하고 해서 학습곡선을 그리도록 만든다.
학습곡선 적용
위에서 만든 학습곡선을 적용했다.
#학습 곡선그리기
cv = ShuffleSplit(n_splits = 100, test_size = 0.2, random_state = 42)
plot_learning_curve(log_reg, knears_neighbors, svc, tree_clf, X_train, y_train, (0.87, 1.01), cv = cv,
n_jobs = 4)
AUC 점수 계산
#분류기마다 roc 곡선 그리기
from sklearn.metrics import roc_curve
from sklearn.model_selection import cross_val_predict
log_reg_pred = cross_val_predict(log_reg, X_train, y_train, cv = 5, method = 'decision_function')
knears_pred = cross_val_predict(knears_neighbors, X_train, y_train, cv = 5)
svc_pred = cross_val_predict(svc, X_train, y_train, cv = 5, method = 'decision_function')
tree_pred = cross_val_predict(tree_clf, X_train, y_train, cv = 5)
#AUC 점수 계산
from sklearn.metrics import roc_auc_score
print('Logistic Regression: ', roc_auc_score(y_train, log_reg_pred))
print('KNears Neighbors: ', roc_auc_score(y_train, knears_pred))
print('Support Vector Classifier: ', roc_auc_score(y_train, svc_pred))
print('Decision Tree Classifier: ', roc_auc_score(y_train, tree_pred))

네 분류기의 ROC 곡선 겹쳐서 그리기
#ROC 곡선 그리기
log_fpr, log_tpr, log_threshold = roc_curve(y_train, log_reg_pred)
knear_fpr, knear_tpr, knear_threshold = roc_curve(y_train, knears_pred)
svc_fpr, svc_tpr, svc_threshold = roc_curve(y_train, svc_pred)
tree_fpr, tree_tpr, tree_threshold = roc_curve(y_train, tree_pred)
def graph_roc_curve_multiple(log_fpr, log_tpr, knear_fpr, knear_tpr, svc_fpr, svc_tpr, tre_fpr, tree_tpr):
plt.figure(figsize = (16, 8))
plt.title('ROC Curve \n Top 4 Classifiers', fontsize=18)
plt.plot(log_fpr, log_tpr, label = 'Logistic Regression Classifier Score: {:.4f}'.format(
roc_auc_score(y_train, log_reg_pred)))
plt.plot(knear_fpr, knear_tpr, label='KNears Neighbors Classifier Score: {:.4f}'.format(
roc_auc_score(y_train, knears_pred)))
plt.plot(svc_fpr, svc_tpr, label='Support Vector Classifier Score: {:.4f}'.format(
roc_auc_score(y_train, svc_pred)))
plt.plot(tree_fpr, tree_tpr, label='Decision Tree Classifier Score: {:.4f}'.format(
roc_auc_score(y_train, tree_pred)))
plt.plot([0, 1], [0, 1], 'k--')
plt.axis([-0.01, 1, 0, 1])
plt.xlabel('False Positive Rate', fontsize = 16)
plt.ylabel('True Positive Rate', fontsize = 16)
plt.annotate('Minimum ROC Score of 50% \n (This is the minimum score to get)', xy = (0.5, 0.5),
xytext = (0.6, 0.3), arrowprops = dict(facecolor = '#6E726D', shrink = 0.05))
plt.legend()
graph_roc_curve_multiple(log_fpr, log_tpr, knear_fpr, knear_tpr, svc_fpr, svc_tpr, tree_fpr, tree_tpr)
plt.show()
내용이 지나치게 많아져서 여기서 일단 마무리하고.. 뒷 내용은 다음에 포스팅 해야겠다.
남은 단계는
3-5) 로지스틱 회귀모형 더 깊게 이해하기
3-6) SMOTE를 활용한 오버샘플림
4-1) 로지스틱 회귀모형으로 검증(Test)
4-2) 신경망으로 검증(언더샘플링과 오버샘플링 비교)
네 단계만 남았으니 좀 더 수월할 것 같다..
솔직히 점점 뒤로 갈수록 지치고 눈이 풀려서 성의없게도 생략한 부분이 많아진 것 같다.
이렇게 가독성이나 전달력도 떨어지는 포스팅을 굳이 따라올 사람은 없을 것 같지만,,
누군가 조금이나마 참고할만한 내용으로 도움이 되면 좋겠다...
'언어 > Python' 카테고리의 다른 글
| 11/13 배운점보다 의문점 (가상환경 경로 문제 어떡하지..) (0) | 2022.11.13 |
|---|---|
| [kaggle] Credit Card Fraud Detection 코드 보고 연습 (2) (0) | 2020.12.19 |
| [Python] 파이썬에 tensorflow 설치하기 (매우 간단) (0) | 2020.12.16 |
| [Python] imblearn 패키지 설치 (매우 간단) (0) | 2020.12.16 |
| [개념] Python Numpy에 대해 이해해보자 3 (array 데이터자료형, 자료형 지정, 형식 변환, 기본 자료형과 Numpy 자료형의 차이) (0) | 2020.08.30 |

