[개념] Python Numpy에 대해 이해해보자 2 (seed지정, size옵션, 이산형, 연속형 확률분포에서 무작위 난수 생성, 간단한 히스토그램 만들기)

Python Numpy에 대해 이해해보자 1

[개념] Python Numpy 패키지에 대해 이해해보자 1 (array 생성, 배열, 차원, dtype 확인, .zeros, .ones, .empty,

이전에 Numpy 패키지의 Array 클래스에 관해 공부했다.

 

오늘은 생각보다 자주 활용되는 무작위 난수 생성 모듈인 numpy.random에 대해 알아보자.

---

먼저 오늘의 공부는 rfriend.tistory.com/284?category=675917

[Python NumPy] 무작위 표본 추출, 난수 만들기 (random sampling, random number generation)

위의 블로그 내용을 참고, 고대로 따라했다.

 

 

1.  Seed 생성 (np.random.seed(seed = 숫자)

 

프로그램이 난수를 생성할 때 무작위로 seed 값 중 하나를 골라 그 seed의 난수생성표에 나온대로 난수를 생성하는 것이라고 알고있다.

 

그래서 만약에 특정 seed로 고정을 해준다면, 난수를 반복해서 생성하더라도 같은 값이 생성된다.

 

#seed 생성

np.random.seed(seed = 100)
np.random.normal(size = 5)

 

보다시피 반복해서 수행해도 같은 난수가 생성된다.

반면 seed를 지정해주지 않으면, 명령을 실행할 때마다 난수가 다르게 생성된다.

 

#without seed

np.random.normal(size = 5)

seed를 지정해주지 않으면 이렇게 무작위로 난수가 생성된다.

 

---

2. size 옵션

 

size 옵션을 활용해 난수를 array클래스로 생성할 수 있다.

 

#size 옵션을 사용해 난수를 array클래스로 생성 가능

np.random.normal(size = (2,3))

np.random.normal(size = (2,3,4))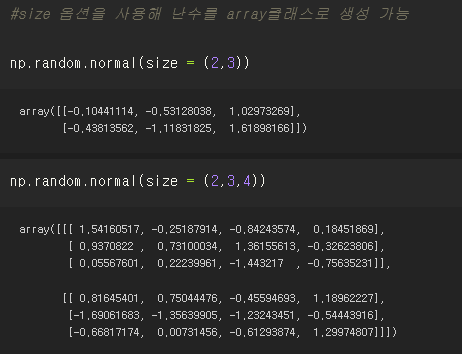

size 옵션을 사용해 2*3, 2*3*4 배열로 난수를 생성했다.

---

3. 다양한 분포에서의 난수 생성

 

numpy 패키지는 다양한 분표에 맞는 난수 생성을 지원한다.

 

대표적으로 정규분포, 이항분포 등이 있겠다.

 

가능한 분포를 모두 적고 한번에 보는 것이 나을 것 같다.

 

먼저 가능한 이산형 확률분포는

 

1. 이항분포 np.random.binomial(n, p, size)
2. 초기하분포 np.random.hypergeometric(ngood, nbad, nsample, size)
3. 포아송분포 np.random.poisson(lam, size)
4. 이산형 균등분포(정수형) np.random.randint(low, high, size)

연속형 확률분포는

 

1. 정규분포 np.random.normal(평균, 표준편차, size)
2. t-분포 np.random.standard_t(df, size)
3. 균등분포 np.random.uniform(low, high, size)
4. F-분포 np.random.f(dfnum, dfden, size)
5. 카이제곱분포 np.random.chisqure(df, size)

이렇게 존재한다.

 

모든 난수생성 함수는 np.random.분포이름의 형태를 가지고 있고, 뒤의 옵션들은 지정해주는 것이 좋다.

 

난수생성 자체가 어려운 것은 아니므로 간단히 활용할 수 있을 것이다.

---

3. 이산형 확률분포

 

3-1. 이항분포 np.random.binomial(n, p, size)

 

#이산형 확률분포에서 난수생성하기
#이항분포 np.random.binomial(n, p, size)
#n은 나올 수 있는 정수, p는 나올 확률, size = 추출횟수

np.random.binomial(1, 0.5, 10)

#p에 가깝게 추출되는지 확인
sum(np.random.binomial(1,0.5,1000) == 1)/1000

1000번 반복한 결과 0과 1중에서 1이 나올 확률은 0.498로 0.5에 근사

---

3-2. 초기하분포 np.random.hypergeometric(ngood, nbad, nsample, size)

 

초기하분포에 대한 이해가 필요한데, 성공확률이 p, 크기가 N인 모집단에서 n개를 비복원추출했을 때 성공이 일어날 횟수X에 관한 내용이다. (솔직히 안 다룬지 좀 돼서 까먹음)

 

위의 함수에서 ngood은 good의 개수, nbad는 bad의 개수고, 전체 크기는 ngood+nbad이다.

 

이 중에서 nsample개만큼 비복원추출할 때 ngood이 몇 개가 나오는지를 확인하는 것을 size번 반복하는 것이다.

 

(대충 이해하고 넘어가자..)

 

#초기하분포 np.random.hypergeometric(ngood, nbad, nsample, size)

np.random.hypergeometric(5,20,5,10)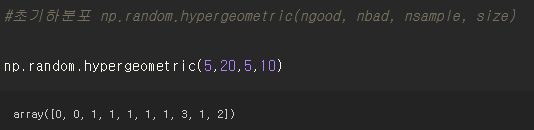

오 의외로 나오기 힘든 3이 한 번 나왔다.

---

3-3. 포아송분포 np.random.poisson(lam, size)

 

포아송분포는 일정 시간 혹은 공간 등에서 사건이 발생하는 평균 횟수인 lambda를 정해준다.

 

만약 한 콜센터에 한 시간동안 전화가 평균 10건 온다면, lambda = 10이다.

 

이 때 x는 한 시간동안 전화가 몇 번 올 것인가를 의미한다.

 

#포아송분포 np.random.poisson(lam, size)

np.random.poisson(10, 10)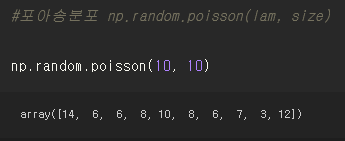

횟수가 늘어나면 늘어날수록 정규분포를 따르게 된다.

#barplot으로 확인

np_po = np.random.poisson(10, 1000)

unique, counts = np.unique(np_po, return_counts = True)

import matplotlib.pyplot as plt
plt.bar(unique, counts)

정규분포스럽다

---

3-4. 이산형 균등분포(정수형) np.random.randint(low, high, size)

 

uniform(균등)분포인데 정수형의 난수를 만들어주는 함수이다.

 

low값부터 high의 정수-1까지 범위에서 무작위로 정수를 추출한다.

 

#이산형 균등분포(정수형) np.random.randint(low, high, size)

num = np.random.randint(0, 11, 100)
num

 

#이산형 균등분포(정수형) np.random.randint(low, high, size)

num = np.random.randint(0, 11, 100000)

#히스토그램

count, bins, ignored = plt.hist(num, bins = 11)

모든 범주가 거의 동일하게 추출되었다.

 

---

4. 연속형 확률분포에서 난수 생성

 

4-1. 정규분포 np.random.normal(평균, 표준편차, size)

 

#연속형확률분포에서 난수 생성
#정규분포 np.random.normal(평균, 표준편차, size)

np.random.normal(0, 1, 100)

#히스토그램으로 분포 모양 살펴보기

rand_norm = np.random.normal(0, 1, 100)

count, bins, ignored = plt.hist(rand_norm)

대충 정규분포 모양이 보인다

---

 

4-2. t-분포 np.random.standard_t(df, size)

 

#t-분포 난수생성 np.random.standard_t(df, size)

rand_t = np.random.standard_t(3, 100)
rand_t

#t-분포 히스토그램

count, bins, ignored = plt.hist(rand_t, bins = 20)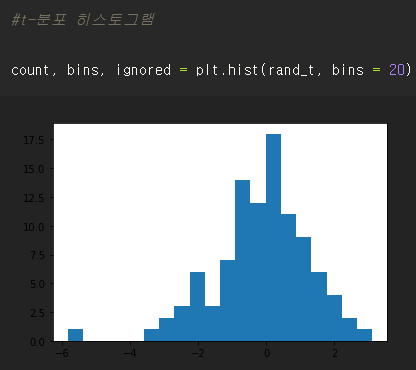

자유도가 3인 t-분포에서 100회 랜덤 추출했을 때 히스토그램

#t-분포 히스토그램 (자유도가 커지면 정규분포를 따름)

rand_t = np.random.standard_t(30, 1000)

count, bins, ignored = plt.hist(rand_t, bins = 20)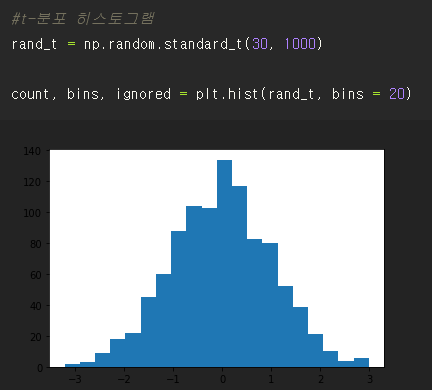

자유도가 커졌을 때 정규분포와 근사한다는 것을 확인

---

4-3. 균등(Uniform)분포 np.random.uniform(low, high, size)

 

보편적으로 많이 쓰는 Unif(0,1) 분포에서 난수를 추출해보자.

 

#균등분포 np.random.uniform(low, high, size)

rand_uni = np.random.uniform(0, 1, 1000)

count, bins, ignored = plt.hist(rand_uni, bins = 20)

low = 0 ~ high = 1 사이의 난수를 추출한다.

---

4-4. F분포 np.random.f(dfnum, dfden, size)

 

dfnum은 분자의 자유도, dfden은 분모의 자유도

 

#F-분포 np.random.f(dfnum, dfden, size)

rand_f = np.random.f(5, 10, 100)

count, bins, ignored = plt.hist(rand_f)

F분포는 오른쪽으로 꼬리가 긴 형태

---

4-5. 카이제곱분포 np.random.chisquare(df, size)

 

#카이제곱분포 np.random.chisquare(df, size)

rand_chi = np.random.chisquare(5, 1000)

count, bins, ignored = plt.hist(rand_chi)

카이제곱 분포도 오른쪽으로 꼬리가 긴 형태

하지만 카이제곱 분포의 자유도가 커지게 되면 정규분포에 근사한다.

#카이제곱분포 np.random.chisquare(df, size), 자유도가 매우 클 때

rand_chi = np.random.chisquare(1000, 1000)

count, bins, ignored = plt.hist(rand_chi)

정규분포에 근사하는 모습을 보인다.

---

오늘은 Numpy 패키지에서 시드를 생성하는 법, size 옵션으로 array클래스로 난수를 생성하는 법과 이산형(이항분포, 초기하분포, 포아송분포, 이산형 균등분포), 연속형(정규분포, t분포, 균등분포, F분포, 카이제곱분포) 확률분포에서 난수를 생성하는 법 그리고 그에 따른 분포를 히스토그램으로 확인하는 법을 살펴보았다.

 

이러한 난수생성은 통계를 공부하면서 분포의 형태를 확인할 때 자주 사용했다.

 

그리고 randint 함수의 정수형 난수 생성을 활용하여 프로그래밍에 사용할 일이 종종 있기 때문에 활용도가 제법 높은 편이다.

 

그러니 까먹지 말고 난수 생성을 하고싶다면 numpy를 떠올리고 random모듈을 써서 원하는 확률분포를 적어 사용하자

 

다음에는 Numpy를 활용한 자료형 변경을 알아보자.