패키지 사용하지 않고 Metropolis-within-Gibbs Sampler 직접 적용하기
논문 : 임상 데이터에 적용하는 베이지안 선형회귀 개론
https://www.sciencedirect.com/science/article/abs/pii/S0005796716302364?via%3Dihub
An introduction to using Bayesian linear regression with clinical data
Statistical training psychology focuses on frequentist methods. Bayesian methods are an alternative to standard frequentist methods. This article prov…
www.sciencedirect.com
위 논문은 베이지안 방법으로 선형회귀 모형을 clinical data (임상 데이터)에 적용하는 방법을 소개하는 논문이다.
학교나 기관 이메일로 로그인하면 걸어둔 링크를 통해 논문을 확인할 수 있고, 데이터 등을 받을 수 있다.
논문에 대한 설명을 간략하게 하자면,
보통 임상 데이터를 분석할 때 Frequentist 방식을 많이 사용하는데
Frequentist 방식의 한계와 베이지안 방식의 장점을 설명하고,
베이지안 방식의 기본 아이디어와 용어들을 간략하게 소개한 후,
어떻게 임상 데이터에 베이지안 방법을 적용할 수 있는지를 설명한다.
논문에 사용한 데이터 : ERN - 뇌파 음성반응 수치 데이터
논문에서는 ERN 데이터라는 뇌파도에 관련한 수치 데이터를 사용한다.
ERN이라는 데이터를 간단히 설명하자면,
ERN은 ERP라는 뇌파도의 관련된 수치들 중의 하나로, 아주 짧은 시간 안에 일어나는 반응을 수치화 한 것이라고 생각하면 될 것 같다. (개인적인 해석이라 정확하지 않을 수 있음)
강박증, 불안 증세, PTSD를 겪는 환자한테서 ERN 수치가 일반인보다 더 큰 폭으로 나타난다는 주장을 검증하고자 환자들과 대조군을 포함한 총 81명에게 STAI라는 불안 증상에 관한 40문답을 진행한 후 그 검사 결과를 Anxiety라는 수치로 수치화하여 독립변수로 설정했다.
데이터의 구조는 매우 간단하다.

먼저, 종속변수인 ern_mean 수치가 주어져있다.
독립변수로는 수치형 변수인 anxiety 지수와 Covariate(공변량)으로 명목형 변수인 성별변수(1: 여성, 0: 남성)를 사용한다.
ERN 데이터에 적용하고자 하는 모형 : 베이지안 방식의 선형회귀 모형
먼저, 베이지안 방법을 위해서는 데이터에 대한 사전지식이 필요한데 논문에 자세한 설명이 나와있다.

ERN 데이터에 적용하고자 하는 가장 기본적인 회귀모형이다.
Model 1은 공변량인 성별변수를 사용하지 않고 독립변수인 anxiety만을 사용하고 있다.
베이지안 방법을 사용하고 있어서 일반적인 회귀모형과 다르게 우리가 사용할 ERN 데이터의 평균과 표준편차가 어떤 분포를 따르고 있다고 본다.
beta0와 beta1, sigma에 대한 분포가 먼저 제시되어 있는데 이 분포를 prior distribution (사전분포)라고 한다.
우리는 사전분포와 Likelihood function (우도 함수)를 사용해서 posterior distribution (사후분포)를 계산해야한다.
다행히도 R에서는 이런 수고로움을 덜어주는 패키지들이 많아서 직접 계산하지 않아도 알아서 문제를 해결한다.
실제로 논문에서도 R에서도 사용할 수 있는 Stan이라는 프로그램의 brms 패키지를 사용한다.
이를 사용하면 간단하게 아래의 결과를 얻을 수 있다.

하지만 패키지에 의존하지 않고 MCMC 방법이 어떻게 돌아가는지 이해할 겸 직접 사후분포를 계산하고 그 분포를 바탕으로 모델을 추정해보려고 한다.
여기에 베이지안 이론 설명을 하고싶지만 잘 설명할 자신이 없어서 넘어가겠다.
(나중에 베이지안 이론을 공부하면서 포스팅 해보겠다)
베이지안 추론을 위한 과정 : 사후분포 계산
베이지안 방법을 적용하기 위해서 사후분포를 계산해야 한다고 했다.
위에서 주어진 모형을 기반으로 사후분포를 계산해보면 아래 식을 구할 수 있다.

사후분포는 관측치 y들이 주어졌을 때 모수들의 분포가 마지막의 식 형태를 띔을 의미한다.
마지막 식의 형태를 띈다고 표현한 것은 사후분포를 계산할 때 곱해진 상수들은 전부 제거하고 비례한 식의 형태를 봄으로써 어떠한 분포를 따른다고 판단하기 때문이다.
비례한 식의 형태가 어떤 분포를 따른다면 사후분포가 결국 그 분포를 따른다는 이해가 필요하다.
아 참 그리고 우리는 각 모수들이 서로 독립이라고 가정한다.
(만약 모수들끼리 서로 독립이 아니라면 joint pdf를 따로 계산해야 하는데 더 복잡해질 것이다)
사후분포를 구했다고 끝난 것은 아니다.
우리가 구하고자 하는 것은 각 모수들에 대한 추정치다.
그래서 우리는 conditional posterior distribution, 즉 조건부 사후분포를 계산해야한다.
한 번 더 계산해야한다는 사실에 지칠 수도 있겠지만 조건부 사후분포 계산은 생각보다 간단하다.
왜냐하면 계산하고자 하는 모수를 제외한 나머지 모수들은 전부 우리가 아는 constant로 취급하기 때문에, 각 모수들을 constant 처리하면 된다.
위 모형에서 모수는 beta0, beta1, sigma이므로 세 가지 조건부 사후분포를 구할 수 있다.
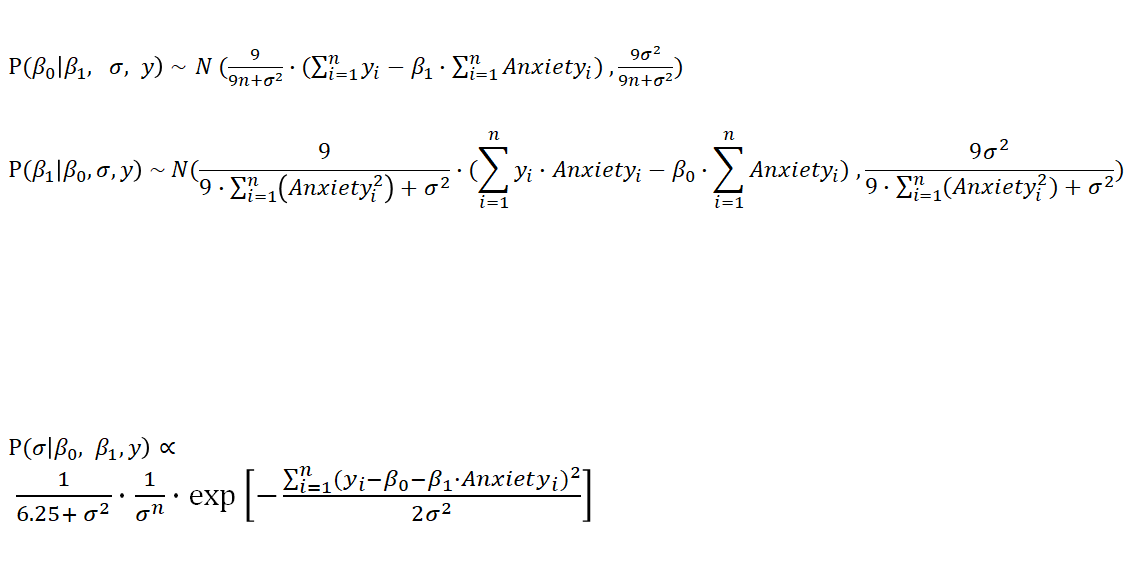
조건부 분포를 사용하는 이유와 Gibbs Sampling에 대한 간단한 설명
(Gibbs Sampler for beta0 & beta1)
위에서 계산한 조건부 사후분포 식을 보면 beta0와 beta1의 분포는 정규분포를 따른다는 것을 알 수 있다.
만일 beta0와 beta1의 경우처럼 추정하고자 하는 모수가 특정 분포를 따른다면,
우리는 그 모수를 추정할 때 R에 있는 분포에서 샘플링 해주는 함수 (ex. rnorm, rchisq 등등)를 이용하면 되기 때문에 모수의 추정이 매우 간단해진다.
예를 들어, beta0 조건부 사후분포는 정규분포를 따르는데 분산으로 9sigma^2/(9n+sigma^2)를 사용하고 있다.
(평균식은 적기 귀찮아서 생략)
그러면 R에서는 beta0 <- rnorm(1, 평균식, 9*sigma^2/(9*n+sigma^2) 요런 식으로 beta0로 추정되는 값을 하나씩 샘플링할 수 있게 된다.
이렇게 샘플링을 반복해서 얻은 beta0 값들의 평균을 구하면 그것이 바로 MCMC로 구한 beta0의 추정치가 되는 것이다.
많은 부분이 생략되었지만 대충 이 방법을 Gibbs Sampling이라고 한다.
말이 나왔으니 Gibbs Sampling에 대해 간단히 설명하자면, Gibbs Sampling을 조건부 분포에서 샘플링한다는 것이 특징이다.
beta0의 경우 beta1, sigma, y가 조건부로 붙어있는데, 이 값들이 주어져야만 beta0를 계산할 수 있다.
마찬가지로 beta1은 beta0, sigma, y를 조건부로 갖는데, 이 값들이 주어져야만 beta1을 계산할 수 있다는 뜻이다.
그리고 Gibbs Sampling이란 맨 처음 단계에는 모든 모수(여기서는 beta0, beta1, sigma)의 초기값을 임의로 설정해서 한 모수를 먼저 Sampling하고(어떤 모수를 먼저 추정할 것인지 순서는 별로 상관이 없다. 지금은 beta0라고 생각하자), 그렇게 Sampling된 모수(beta0)를 다음 모수(beta1)에 반영해서 다음 모수(beta1)를 Sampling하고, 또 다음 모수(sigma)에는 그 전에 Sampling된 모수들(beta0, beta1)의 값을 반영해서 샘플링하는 방식의 연속적인 알고리즘을 갖게된다.
이렇게 반복 샘플링된 각 모수들의 샘플을 저장해서 그 평균을 구하면 그것이 바로 우리가 구하고자 하는 모수의 추정치다.
Metropolis Hastings (M-H Sampler) for Sigma
beta0와 beta1의 경우 조건부 사후분포 계산 결과 정규분포의 형태를 띄어서 정규분포에 적용할 수 있었다.
하지만 sigma처럼 어떠한 분포를 따른다고 할 수 없는 not closed form으로 계산된다면 문제가 복잡해진다.
특정 분포에서 샘플링이 불가능하기 때문에 간접적으로 모수를 추론하는데 이 때 가장 basic한 방법을 Metropolis Hastings Sampling이라고 한다.
다른 말로 Metropolis Sampler 혹은 줄여서 M-H라고도 하고 Sampling 대신 그 방식을 알고리즘이라고 말하기도 하며, M-H 자체도 하나의 방법이지만 또 M-H 안에 다양한 알고리즘이 또 포함되어 있어서 Gibbs Sampling, Random walk Metropolis Sampling, Independence Sampling 등도 다 M-H의 한 종류라고 볼 수 있는 것으로 보인다.
M-H Sampler의 가장 큰 특징은 Proposal distribution을 도입한다는 것이다. (뭐라고 번역해야할지 모르겠다. 제안분포?)
M-H에서 Proposal distribution은 우리가 target 분포와 비교해서 proposal 분포가 더 괜찮으면 proposal 분포에서 sampling한 값을 사용하고, 그게 아니라면 이전 target 분포에 쓰인 값을 그대로 쓰도록 한다.
그리고 위의 방식이 연속된다면 MCMC가 적용된 M-H 방식의 알고리즘이라고 볼 수 있다.
설명을 조금만 더 해보자면 우선 우리가 구하고자 하는 모수의 분포를 이제 target distribution이라고 칭한다.
target distribution이 특정 분포를 따르지 않는 것이 문제인데, 식과 가능한 모수의 범위 정도를 뜯어보면 대충 target이 어떤 형태를 띄겠다는 짐작이 가능하게 된다.
그렇게 target 분포의 모양이나 범위로 짐작한 분포 형태를 Proposal distribution으로 도입한다.
그러면 우리는 Proposal과 이전 target 분포에 쓰인 값 중 어떤 것이 더 나은 값인가를 Acceptance, Rejection 규칙을 설정해 비교한다.
그 과정을 N번 반복하여 Proposal 분포의 값을 채택하거나, 기각하는 과정을 N번 반복한 것이 바로 M-H Sampling이다.
거기서 구해진 Sampling 값들만을 저장하여 이것들의 평균을 구하면 그것이 바로 베이지안의 MCMC 방식에서도 특히 M-H 방식으로 sampling된 모수의 추정치로 여긴다.
처음 M-H 알고리즘을 적용하고자 하면 Proposal distribution을 뭐로 잡아야 하는지 전혀 감이 오지 않을 것이다.
함수식을 전개를 못하고 어떤 분포를 따르는지 모르는데 어떻게 우리가 맘대로 Proposal distribution을 설정하라는 것인지 판단하기가 어려운데, 이는 거의 경험에 의존하는 것으로 보인다.
실제로 모수의 범위가 (- Inf, + Inf) 라면 Proposal 분포로 정규분포를 많이 사용하고,
모수의 범위가 (0, + Inf)라면 그 범위와 유사한 Inverse-Gamma 분포를 많이 사용한다.
또 만약 모수가 correlation인 경우 그 범위는 (-1, +1)이 되는데 이런 범위를 갖는 분포가 잘 없어서 보통 Uniform(-1, 1)을 사용하면 되겠다고 판단한다.
이처럼 Proposal을 선정하는 근거는 대단한 근거가 있는 것이 아니라 대충 모수 범위를 보고 경험적으로 판단하는 것에 불과하다.
따라서 우리도 Proposal distribution을 설정할 때 대강 경험적으로 판단하면 된다.
Sigma에 사용할 Proposal distribution은?
논문에서 Sigma의 사전분포로 Half-Cauchy 분포를 제시했다.
Sigma는 정규분포의 표준편차이므로 0보다 커야해서 다양한 분포 중에서도 0보다 큰 값만을 갖는 분포를 선정해야 한다.
일반적으로 Inverse-Gamma 분포를 사용하지만 논문에서는 inverse-Gamma가 표본이 적을 때 극단적인 값에 큰 가중치를 갖는 것을 견제하고자 Half-Cauchy를 사용하는 것이 더 좋겠다고 판단했다고 한다.
사전분포로 Half-Cauchy를 사용했기 때문에 Proposal도 Half-Cauchy를 사용하는 것이 좋을 수 있겠다는 생각이 들었다.
또한, Half-Cauchy와 유사한 Half-Normal 분포도 존재하는데 이 분포도 Proposal로 사용해보기로 했다.
R 코드로 M-H Sampling 구현
데이터를 불러온 다음 우선 우리가 계산할 sigma 함수를 정의해주었다.
sigma의 조건부 사후분포를 직접 function으로 만들어주면 된다.
근데 sigma의 식을 그대로 코드를 구현해보니 sigma의 식에서 사용된 지수함수에 50 정도로 조금만 큰 값이 들어가도 바로 Infinity로 발산해 버리는 문제가 있었다.
이 문제를 해결하기 위해 보통 Acceptance-Rejection Rule로 사용하는 식 전체에 log를 사용해서 그 값을 변환하는 방식을 쓰는 것 같았다.
그래서 sigma의 식 전체에도 log를 씌워주는 것이 맞다고 생각되어 log를 씌운 sigma 식을 계산하여 function으로 만들었다.
# Compute each summation to get sigma function
y1 = sum(ern_mean); a = sum(anxiety); s = sum(sex)
y2 = sum(ern_mean^2); a2 = sum(anxiety^2); s2 = sum(sex^2)
ya = sum(ern_mean*anxiety); ys = sum(ern_mean*sex); as = sum(anxiety*sex)
a2s = sum(anxiety^2*sex); as2 = sum(anxiety*sex^2); a2s2 = sum(anxiety^2*sex^2)
yas = sum(ern_mean*anxiety*sex)
### Define log_sigma_f1 function for model 1
log_sigma_f1 <- function(beta0, beta1, sigma){
-n*log(sigma)-log(6.25+sigma^2)-(y2+beta0^2*n+
beta1^2*a2-
2*beta0*y1-
2*beta1*ya+
2*beta0*beta1*a)/(2*sigma^2)
위에서 변수 간 곱한 값의 summation을 각각 계산한 것은 log를 취한 sigma식을 전개해서 구하는 것이 더 편하겠다는 판단 하에 미리 계산해 준 것이다.
그리고 현재 진행하고 있는 model1 뿐만 아니라 model2, model3도 구현하기 위해 저렇게 다양한 변수 간 곱들의 합을 먼저 구해주었다. (하지만 이 포스팅에는 model1만 포스팅할 것이다.
R로 Metropolis-within-Gibbs Sampling (MWG) 적용하는 법은?
갑자기 Metropolis-within-Gibbs (MWG)는 또 뭔 말인가 싶을 수도 있는데 말만 좀 바뀐 것이지 beta0와 beta1의 sampling을 위해 Gibbs Sampling을 진행하고, sigma의 sampling을 위해 M-H Sampling을 적용하는 것을 좀 더 그럴싸하게 말한 것이라고 생각하면 될 것 같다. (이 부분이 사실 정확하지는 않은데 나는 그렇게 이해했다.)
Gibbs Sampling을 할 때 beta0, beta1, sigma를 한 코드 내에서 Sampling하게 되고 beta0, beta1처럼 sampling이 쉬운 경우와 달리 sigma처럼 not closed form인 경우 M-H를 따로 돌리는 코드를 포함해서 Gibbs 코드 안에서 돌려야 한다.
이것을 MWG라고 따로 멋드러진 칭호를 정해서 부를 수도 있지만,
정말 수많은 대부분의 경우가 이런 식이라 굳이 MWG라고 말하지 않고 보통 그냥 Gibbs Sampling을 썼다고 퉁치는 것 같다.
어쨌거나 중요한 점은 beta0, beta1은 평범한 Gibbs Sampling, sigma는 M-H Sampling으로 Sampling해서 샘플링 된 값들의 평균을 모수들의 추정치라고 판단하는 것이다.
##########################################
# Set iterations and Burn-in
N = 4000; burn = N/2
##########################################
##### Model 1
para1 = matrix(1, N, 3) # parameter matrix for model 1
k1 = 0
### Model 1 : Generate the chain
for (i in 2:N){
beta0 = para1[i-1, 1]
beta1 = para1[i-1, 2]
sigma = para1[i-1, 3]
# beta0 - Gibbs
para1[i, 1] = rnorm(1, 9*(y1-beta1*a)/(9*n+sigma^2),
sqrt(9*sigma^2/(9*n+sigma^2)))
# new beta 0
beta0 = para1[i, 1]
# beta1 - Gibbs
para1[i, 2] = rnorm(1, 9*(ya-beta0*a)/(9*a2+sigma^2),
sqrt(9*sigma^2/(9*a2+sigma^2)))
# sigma - MH sampler
beta1 = para1[i, 2] # new beta2
sigmat = para1[i-1, 3]
# Proposal: Half-cauchy
y = rhalfcauchy(1, sigmat)
lognum = log_sigma_f1(beta0, beta1, y) + log(dhalfcauchy(sigmat, y))
logden = log_sigma_f1(beta0, beta1, sigmat) + log(dhalfcauchy(y, sigmat))
#y = rhalfnorm(1, sqrt(pi/2)/sigmat) # Proposal: Half-normal
#lognum = log_sigma_f1(beta0, beta1, y) + log(dhalfnorm(sigmat, sqrt(pi/2)/y))
#logden = log_sigma_f1(beta0, beta1, sigmat) + log(dhalfnorm(y, sqrt(pi/2)/sigmat))
if (log(runif(1)) <= lognum-logden) para1[i, 3] <- y
else {
para1[i, 3] <- sigmat
k1 <- k1+1
}
}
처음 코드를 짤 때는 힘들었는데 짜다보니 Gibbs와 M-H Sampling의 프로세스가 훨씬 더 잘 이해되었다.
위에서 총 iteration 횟수는 4000번으로 지정해주었다.
M-H를 포함하고 있는 베이지안의 MCMC 방식은 결국 iteration으로 밀어붙이는 것이므로 그 횟수가 많을수록 추정치가 더 정확해지므로 여유가 된다면 100,000번 정도는 해주면 좋다.
Burn-in-period (버리는 구간)
코드를 보면 N번의 iteration을 거듭하면서 초기값에서 점차 추정치로 수렴하게 된다.
그런데 초기값 근처의 iteration은 마지막 평균을 구할 때 포함시키기에는 좋지 않은, 이상치에 가까운 수치이다.
우리는 그러한 좋지 않은 수치를 버리고 싶어서 burn-in-period라는 구간을 정해서 이 구간에서 Sampling된 값들은 추정에 사용하지 않는다.
보통 burn-in period는 1부터 1000 혹은 2000 사이의 값으로 지정해주면 좋지 않은 수치들을 충분히 버릴 수 있게 된다.
따라서 만약 iteration을 100,000번 돌릴 때에는 burn-in-period를 이 코드에서처럼 N/2를 쓰지는 말고 따로 수치를 정해주는 것이 좋다.
Initial value의 설정 (초기값 설정)
나는 para1 = matrix(1, N, 3)라는 코드를 사용했다.
이 말은 para1이라는 이름의 행렬을 만들건데 4000x3의 행렬을 만들고 그 원소를 전부 1로 하는 행렬을 만들라는 뜻이다.
그리고 for문 내부를 보면 매 iteration마다 반복 수행할 코드가 정해져있다.
beta0 = para1[i-1, 1]
beta1 = para1[i-1, 2]
sigma = para1[i-1, 3]여기서는 매 반복마다 beta0, beta1, sigma라는 argument(인수)를 para1의 이전 행의 각 칼럼 원소를 사용하라는 뜻이다.
Beta0, Beta1 Gibbs Sampling으로 샘플링
# beta0 - Gibbs
para1[i, 1] = rnorm(1, 9*(y1-beta1*a)/(9*n+sigma^2),
sqrt(9*sigma^2/(9*n+sigma^2)))
위에서 지정한 beta0, beta1, sigma를 사용해서 정규분포에 대입했다.
그리고 그 값을 para1의 이번 행 첫번째 칼럼의 원소로 저장한다.
beta0 = para1[i, 1]
이제 beta0 인수로는 이번에 계산한 값을 사용하라는 뜻이다.
beta1도 똑같은 과정으로 진행된다.
Sigma를 M-H Sampler로 샘플링
# Proposal: Half-cauchy
y = rhalfcauchy(1, c1*sigmat)
lognum = log_sigma_f1(beta0, beta1, y) + log(dhalfcauchy(sigmat, y))
logden = log_sigma_f1(beta0, beta1, sigmat) + log(dhalfcauchy(y, sigmat))여기서 y에 쓰인 rhalfcauchy가 바로 누누히 언급했던 Proposal distribution이다.
그리고 그 아래에 lognum과 logden이라는 식은 위에서 언급한 Acceptance-Rejection Rule(AR Rule)에 사용될 분수에 log를 취한 것이다.
원래는 num/den이라는 분수식이 AR Rule에 사용되는 식인데 여기에 로그를 취해서 log(num)-log(den)로 꼴이 바뀌게 되었다.
Acceptance-Rejection Rule (AR Rule)
if (log(runif(1)) <= lognum-logden) para1[i, 3] <- y
else {
para1[i, 3] <- sigmat
k1 <- k1+1
}이게 바로 AR Rule이다.
num/den을 구한 값이 균등분포(0, 1)에서 무작위 샘플링한 값도가 크거나 같으면? -> Proposal distribution에서 구한 y를 Accept
num/den을 구한 값이 균등분포(0, 1)에서 무작위 샘플링한 값도가 작으면? -> 이전 iteration에서 사용한 sigma 값을 현 iteration의 sigma에도 그대로 사용 (즉, y는 rejected)
이러한 규칙을 Acceptance-Rejection Rule이라고 한다.
위에 제시한 전체 과정을 반복하며 para1 행렬에 새로운 값들이 저장된다.
Check Result
이제는 우리가 추정한 결과를 정리해서 살펴볼 차례다.
# Check the samples
head(para1, 50)
# Eliminate burn-in period
parameter1 = para1[(burn+1):N,]
# Check mean, sd and quantiles
mean1 = round(colMeans(parameter1), 4)
sd1 = round(sqrt(diag(cov(parameter1))), 4)
prob = c(0.025, 0.5, 0.975)
lb1 = md1 = ub1 = numeric(ncol(parameter1))
for (i in 1:ncol(parameter1)) {
lb1[i] = round(quantile(parameter1[, i], probs = prob)[1], 4)
md1[i] = round(quantile(parameter1[, i], probs = prob)[2], 4)
ub1[i] = round(quantile(parameter1[, i], probs = prob)[3], 4)
}
# Make table
coef.model1 = c("beta0", "beta1", "sigma")
model1_result = data.frame(coef.model1, mean1, lb1, ub1)
colnames(model1_result) <- c("coef", "mean", "2.5% perc", "97.5% perc")
model1_result
# Rejection rate & Acceptance rate
data.frame(RR = k1/N, AR = 1-k1/N)
# Traceplot
dev.new()
par(mfrow = c(3, 1))
plot(1:N, para1[, 1],type = "l", main = "beta0")
plot(1:N, para1[, 2],type = "l", main = "beta1")
plot(1:N, para1[, 3],type = "l", main = "sigma")Burn-in-period 제거
burn-in-period는 불필요한 구간이라고 했다.
이 부분을 제거하고 parameter1이라는 새로운 행렬을 만들어준다.
평균, 표준편차, quantile table 만들기
간단하게는 그냥 mean(parameter1[, 1]), sd(parameter1[, 1]) 이라는 기본적인 함수를 써서 평균과 표준편차를 구할 수 있다.
하지만 나는 좀 더 그럴싸해보이려고 colMeans(), cov() 함수를 사용했다.
quantile 계산에 for문을 돌린 맥락도 마찬가지다.
(참고로 quantile값은 베이지안의 Credible Interval (CrI)을 구하는 가장 간단한 방법 중 하나이다. Credible Interval은 Frequentist의 Confidence Interval(CI)과 유사한 개념이지만 해석은 다르다.)
모든 값들을 정리해서 새로운 데이터프레임으로 만들어주었다.

내 테이블을 논문의 결과와 비교해보자.

모든 계수들의 추정치와 quantile값이 크게 차이나지 않았다.
논문에서는 Stan이라는 프로그램의 다른 패키지를 사용해서 구한 추정치인데 거의 유사한 결과를 얻을 수 있었다.
CrI도 거의 유사해서 좋은 결과를 얻은 것 같다.
Rejection Rate & Acceptance Rate (RR and AR)
M-H Sampling에서 얼마나 많은 값이 채택되었는가 혹은 기각되었는가는 우리가 선정한 Proposal distribution의 적절성을 평가할 수도 있고, 샘플의 적절성을 판단하는데 좋은 수치가 된다.

AR은 일반적으로 0.23 ~ 0.44가 최적의 값이라고 알려져있다.
하지만 우리의 AR은 0.079로 매우 낮아 별로 좋지 않은 수치를 가리키고 있었다.
이것을 개선하는 방식은 보통 Adaptive MH라는 방식으로 Proposal distribution의 분산을 조정하여 진행한다.
그런데 안타깝게도 Proposal과 target distribution이 roughly normal인 경우에나 Adaptive MH가 효과적이고 우리가 사용한 half-cauchy처럼 right-skewed인 분포의 경우 달리 좋은 효과를 발휘하지 못한다.
그래서 AR은 이대로 0.079를 사용하는 수밖에 없어 보였다.
어느정도 괜찮은 결과를 보였기 때문에 Iteration을 100,000번으로 늘려서 다시 결과를 확인해보았다.
Model1 : 100,000번 반복해보았다.


100,000번으로 반복 횟수를 늘린 결과, 추정치가 좀 더 정교해진 모양이다.
전체적인 수치가 소폭 개선됨과 동시에 특히 sigma의 추정치나 CrI가 좀 더 유사해진 것 같았다.
Traceplot 확인

mixing이 잘 되었는가는 parameter space를 전체적으로 잘 훑는가이고
stationary는 하나의 값으로 수렴해가는 듯 안정적인 형태를 띄는가를 의미한다.
이는 모두 시각적으로 판단하는 것이라 주관적이지만,
지금 보이는 traceplot은 mixing이 잘 되고, stable하여 잘 converge(수렴)한다고 보아도 좋을 수준이었다.
마무리 - 전체적인 결과에 대한 평가와 느낀 점
수치와 plot들이 성공적인 모수 추론에 성공했음을 말해주었다.
채택률 (Acceptance Rate)이 낮다는 점은 다소 아쉬웠지만 전체적으로 만족스러운 결과를 얻어내었다.
뿐만 아니라 model2와 model3도 모두 model1처럼 좋은 결과를 얻었다.
이번 논문 분석을 통해 베이지안 추론 과정을 드디어 약간 이해한 것 같았고,
M-H와 Gibbs를 직접 코딩하며 그동안 개념으로만 접해 다소 난해하게 느꼈던 모든 용어들 (예를 들자면 Proposal, posterior, conditional posterior, Credible Interval 등등)을 자주 사용하여 체득할 수 있었다.
사실 이는 베이지안의 기초에 불과하지만, 한 마디도 이해 못했던 학부시절이나 개념이 헷갈려 틈틈히 수업 중에도 종종 왜 이걸 배우고 있는지 흐름을 놓치게 됐던 과도기를 조금은 이겨낸 것 같아 뿌듯하다.
추가적으로 Adaptive MH를 쓸 수 없는 이 모형과 같은 경우 AR을 개선할 수 있는 또다른 방법이 있는지 알아보면 좋을 것 같다.
생각보다 논문 분석은 오래 걸리지 않았는데 이를 블로그에 포스팅하는 것이 훨씬 힘들었다.
부족한 지식으로 다른 사람에게 전달할 수준도 아니거니와 글재주도 없어서 좋은 설명을 하지 못한 것 같다.
이번 포스팅은 내 지식을 점검하고자 노력했다는 데에 큰 의의를 두고 싶다.
혹 이 글을 참고하고자 들어오신 분이 있다면 부족한 글을 읽어주셔서 감사하고 죄송하다는 말씀드리고 싶다.
'논문' 카테고리의 다른 글
| 11/02 배운점 (인덱스 추출은 which 함수를 써라) (0) | 2022.11.02 |
|---|---|
| 11/01 LATEX 배운점.. (0) | 2022.11.01 |