Longest Increasing Subsequence (LIS)
최장 부분 증가수열 문제는 DP 문제의 대표적인 문제 중 하나다.
먼저, 문제부터 보자.
※ 문제 출저 (인프런 강의 - 파이썬 알고리즘 문제풀이 입문)
문제
N개의 자연수로 이루어진 수열이 주어졌을 때, 그 중에서 가장 길게 증가하는 원소들의 집합의 길이를 구하라.
입력)
5 3 7 8 6 2 9 4
출력)
4
DP의 조건에 해당하는가
이 문제가 DP에 해당하는지 조건을 따져봐야 한다.
1. Optimal Substructure인가
하위 문제의 최적의 해를 사용하여 전체 최적의 해를 구할 수 있는지 보자.
arr = [5, 3, 7, 8, 6, 2, 9, 4] 라고 하자.
시작은 arr의 가장 왼쪽 값부터 시작한다
우선, 5라는 숫자 하나로 만들 수 있는 최장 수열의 길이는 1이다
그 다음, 3이라는 숫자를 보면 5보다 작은 숫자이므로 앞의 5로 만들 수 있는 수열은 사용할 수 없다
최장 수열의 길이는 1이다
다음 7은 앞의 항으로 5나 3보다 크기 때문에
5로 만들 수 있는 최장 수열의 길이 + 1
3으로 만들 수 있는 최장 수열의 길이 + 1
둘 중에서 길이가 가장 큰 값을 사용할 수 있다
이처럼 하위 문제를 거듭하면서 배열의 뒤쪽으로 갈 수록 하위 문제의 최적 해에 1을 더해가는 구조이므로
Optimal Substructure이다
2. Overlapping Subproblems
동일한 하위 문제가 반복적으로 계산되는가?
→ 그렇다. 7의 값에서 최적해를 구하기 위해 5의 해와 3의 해를 이용하고,
뒤에서 8의 값에서 최적해를 구하기 위해 7, 5, 3에서의 최적해 중 가장 큰 값을 이용한다
즉, 하위 문제에서 계산된 값을 반복해서 계산하는 프로세스가 필요하다.
따라서, 이 문제는 DP 문제다.
실제 문제를 풀 때는 이렇게 고려하기보다 대략적인 감으로 유추해서 바로 DP를 적용하는 모양새로 가야겠다.
DP로 생각하기
DP에 해당함을 깨달았기 때문에 DP, 점화식처럼 생각해야 한다.
1. 답안 초기화
DP로 풀 때는 보통 답안 배열을 초기화 해두고
2. 첫번째 값 입력
첫번째 값은 직접 적어둔다.
(현재 문제를 풀기 위해 하위 문제를 어디까지 불러오느냐에 따라서, 두번째, 세번째 값까지는 직접 계산하여 입력해주어야 할 수도 있다)
3. 두번째 하위 문제부터 점화식 도입 (반복문)
for i in range(1, n + 1):
for j in range(i):
4. 문제의 조건을 세분화하여야 한다.
4-1. 조건 1) 현재 배열의 값이 이전의 값들보다 크다 (arr[i] > arr[j])
4-1-1. 현재 값보다 작은 이전의 값들 중 길이가 가장 큰 내용을 기록해야 한다. (if MAX < dp[j]: MAX = dp[j])
dp[i] = MAX + 1
4-2. 조건 2) 현재 배열의 값이 이전의 모든 값들보다 작다
dp[i] = 1
5. 결과 출력
print(max(dp))
이런 구조로 이해를 해야한다.
LIS 문제의 응용
이런 종류의 수학 문제는 코테에 나오지 않을 것 같지만, 사실 이 개념이 적용된 응용 문제들이 있을 수 있다.
보자마자 LIS 문제네? 라고 생각할 수는 없는데, 사실은 그 개념이 적용된 것이다.
예를 들어 최대 선 연결하기 문제가 있다.
※ 문제 출저 (인프런 강의 - 파이썬 알고리즘 문제풀이 입문)
왼쪽의 번호와 오른쪽의 번호가 있는 그림에서 같은 번호끼리 선을 연결하려고 한다.
왼쪽 번호는 무조건 위에서 차례로 1부터 N까지 오름차순으로 나열되어 있다.
오른쪽의 번호는 무작위로 1부터 N까지의 숫자가 배열되어 있다.
서로 선이 겹치지 않고 최대 몇 개의 선을 연결할 수 있는가?
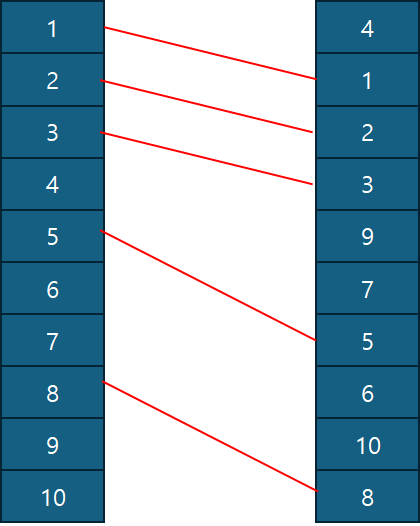
이 문제는 LIS 문제라고 생각이 들지 않지만, 깊게 들여다보면 최장 부분 증가수열을 구한다는 것을 알 수 있다.
같은 숫자끼리 선을 연결해야 하는데,
만일 현재 3이라는 숫자를 보는 와중에 이전 숫자에서 3보다 큰 값이 나오면 선이 겹치게 된다
→ 즉, 이전 숫자는 현재 보고있는 숫자보다 작은 숫자만 와야 한다.
→ 증가수열을 찾는 것인데, 일부 숫자는 건너 뛰어도 된다
→ 부분 증가수열을 찾는 것이고, 그 중 최대값을 찾는 것이기 때문에
→ 최장 부분 증가수열을 찾는 것이다.

이처럼 위 문제를 접근할 때, LIS처럼 할 수 있음에 유의하자


